Inkreis eines Dreiecks – Mathe 7. Klasse

Ein Inkreis ist ein Kreis, der durch alle drei Eckpunkte eines Dreiecks verläuft. In der 7. Klasse Mathematik der Realschule Bayern lernst du wie du diesen mithilfe von Winkelhalbierenden zeichnest oder auch konstruierst.
Jedes Dreieck besitzt einen Inkreis.

Entdecke eine innovative Lernplattform, um Mathe online zu lernen und zu üben: Du findest hier interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

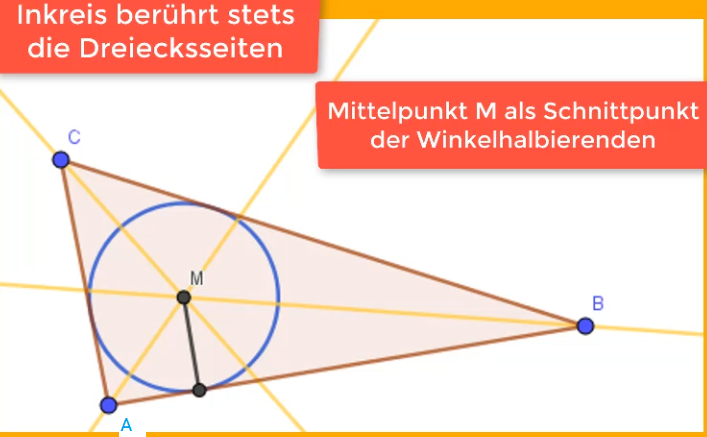
Wie findest du den Inkreismittelpunkt?

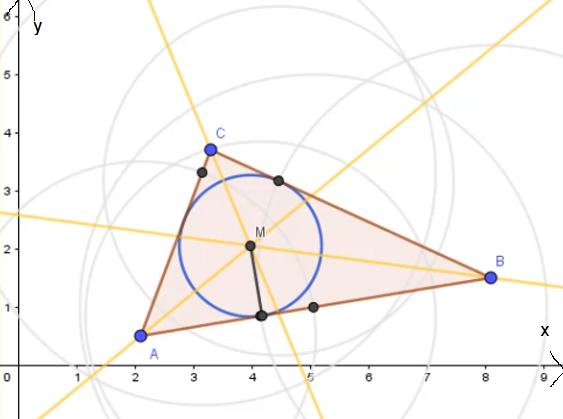
Der Inkreismittelpunkt ist immer der Schnittpunkt der drei Winkelhalbierenden. An sich reicht es aus, wenn du zwei Winkelhalbierenden zeichnest oder konstruierst, um den Mittelpunkt zu erkennen. Die dritte Winkelhalbierende dient als Kontrolle, denn auch diese muss durch den gleichen Schnittpunkt verlaufen. Alle Punkte auf der Winkelhalbierende sind von den beiden Dreiecksseiten (Schenkel des Winkels) gleich weit entfernt. Nachdem diese Eigenschaft auf alle drei Winkelhalbierenden zutrifft, ist auch der Schnittpunkt von allen drei Eckpunkten gleich weit entfernt. Diese Tatsache trifft auf jeden Kreismittelpunkt zu.

Wo befindet sich der Inkreismittelpunkt?

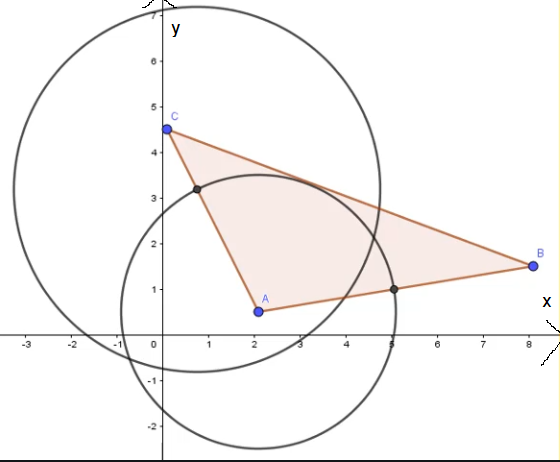
Zeichnest oder konstruierst du zu einem Dreieck einen Umkreis, so hängt die Lage des Umkreismittelpunkts von der Art des Dreiecks ab.

– Bei einem spitzwinkligen Dreieck liegt der Mittelpunkt innerhalb des Dreiecks.
– Bei einem rechtwinkligen Dreieck befindet er sich auf einer Dreiecksseite.
– Bei einem stumpfwinkligen Dreieck liegt der Umkreismittelpunkt außerhalb des Dreiecks.

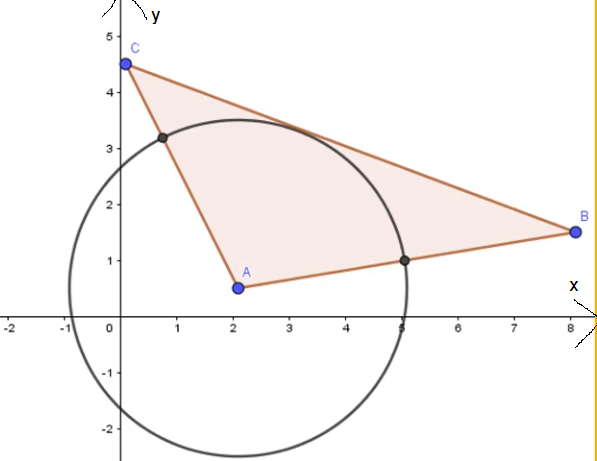
Zeichnest oder konstruierst du hingegen einen Inkreis, so liegt der Inkreismittelpunkt in jedem Dreieck immer innerhalb des Dreiecks.

Merke: Der Inkreismittelpunkt liegt immer innen – der Umkreismittelpunkt nicht. 

Inkreis konstruieren – Schritt für Schritt

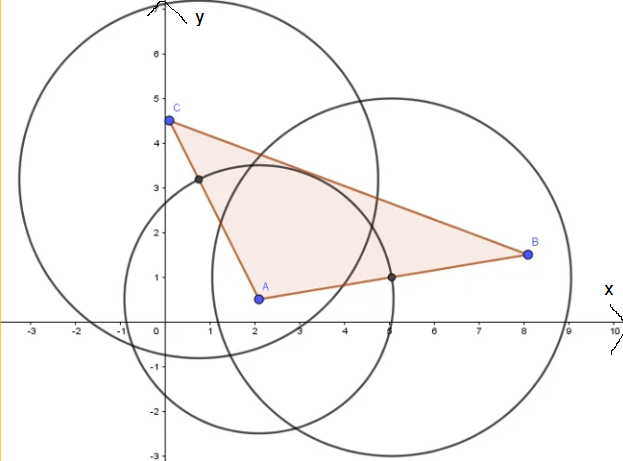
Gegeben ist hier folgendes stumpfwinklige Dreieck ABC.
Ziel ist es, dass du durch die Konstruktion aller drei Winkelhalbierenden die Lage des Inkreismittelpunktes zeichnerisch ermittelst.

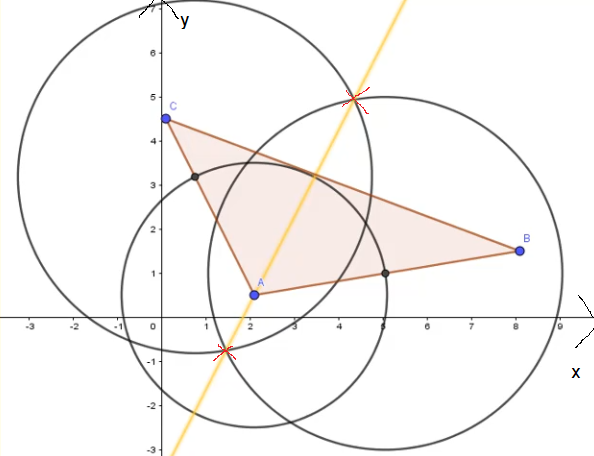
Im ersten Schritt stichst du mit dem Zirkel in den Punkt A ein. Wähle einen beliebigen Kreisradius. Markiere die beiden Schnittpunkte der Kreislinie mit den beiden Schenkeln.

Im zweiten Schritt stichst du nun mit dem Zirkel nacheinander in die beiden Schnittpunkte ein. Wähle erneut einen Kreisradius, der sich vom Radius aus Schritt 1 unterscheiden kann.

Hier im Bild links wurde in einen Schnittpunkt eingestochen und der erste Halbkreis gezeichnet.

Stich nun mit dem gleichen Radius (wie in Schritt 2) in den anderen Schnittpunkt ein und zeichne einen Halbkreis. Die beiden Halbkreise schneiden sich in zwei Punkten. Diese beiden Schnittpunkte werden jetzt gleich für die Winkelhalbierende benötigt.
Zeichne nun die Winkelhalbierende ein. Die farbige Linie stellt die Winkelhalbiernde dar.
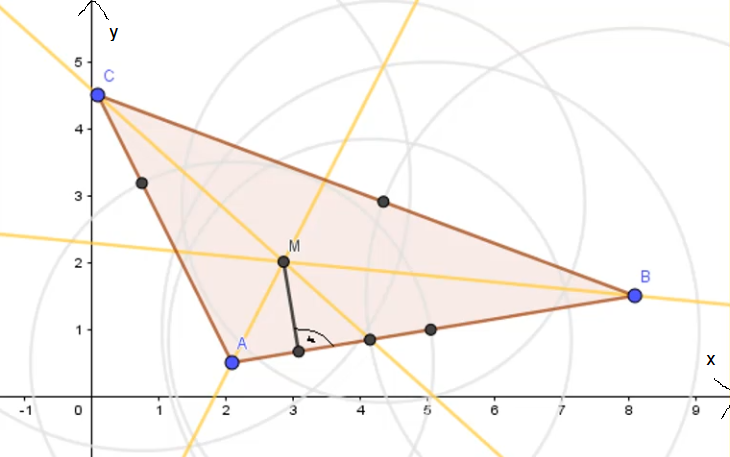
Wende die gleiche Vorgehensweise nun auch für die verbleibenden beiden Winkel an, sodass du drei Winkelhalbierenden konstruiert hast. Zwei Winkelhalbierende genügen, die dritte dient zur Kontrolle.

Stich nun mit dem Zirkel in den Schnittpunkt der Winkelhalbierenden ein. (Inkreismittelpunkt)
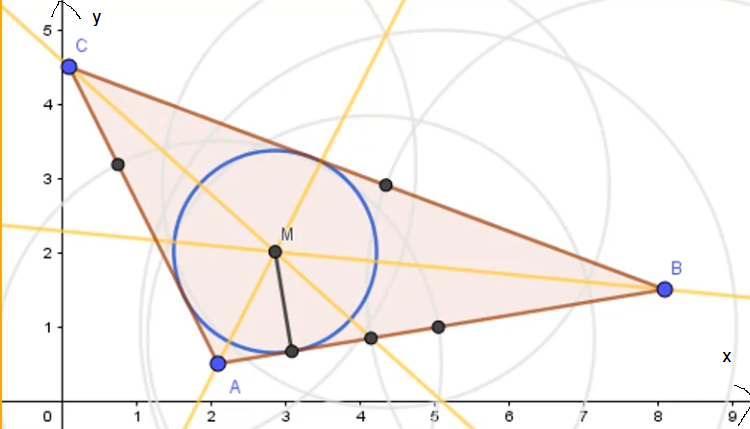
Der Inkreisradius ist der Abstand (kürzeste Entfernung, da rechter Winkel) vom Inkreismittelpunkt bis zu einer Dreiecksseite. Da der Inkreismittelpunkt von allen Dreiecksseiten gleich weit entfernt ist, kannst du den Abstand zu einer der drei Seiten für das Einstellen des Zirkels auswählen.

Zeichne nun den Inkreis ein. Wenn du sauber gezeichnet hast, berührt die Kreislinie alle Dreiecksseiten.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, hilfreiche Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken. Lerne und übe Mathe online.