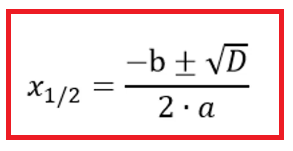Nullstellen einer Parabel berechnen:

Was ist eine Nullstelle?

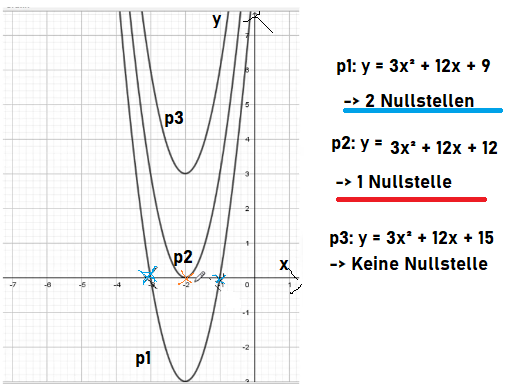
Unter Nullstelle versteht man den Schnittpunkt des Funktionsgraphen mit der x-Achse (deshalb gilt: y = 0). In der 8. Klasse (I Zweig) bzw. 9. Klasse (II/II Zweig) hast du bereits gelernt wie du die Nullstelle einer linearen Funktion berechnest. In der 10. Klasse (II/III) bzw. 9I lernst du nun wie du die Nullstellen einer Parabel berechnest. Manche Parabeln liegen so im Koordinatensystem sodass sich zwei Nullstellen ergeben. Bei anderen hingegen liegt der Scheitelpunkt der Parabel auf der x-Achse, es gibt eine Nullstelle. Und dann gibt es noch den Fall, dass die Parabel die x-Achse nicht schneidet, es gibt hier keine Nullstelle. Die Zeichnung veranschaulicht dir diese 3 möglichen Szenarien. Nun betrachten wir wie diese 3 Möglichkeiten rechnerisch bestimmt werden können.

Auf dieser Lernplattform kannst du Mathe online üben: Du findest Mathe-Lernvideos von einer Realschullehrerin, interaktive Übungen und Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Nullstellen berechnen mit der „Nullstellenformel“ (oder auch „Mitternachtsformel“)

Diese Formel ist sehr bekannt und sollte so gut sitzen, dass du diese selbst dann beherrscht, wenn du aus dem Schlaf gerissen wirst (an Mitternacht).

x1/2 bedeutet, dass du mithilfe dieser Formel die beiden Nullstellen x1 und x2 berechnen kannst. Einmal wendest du diese mit + an und einmal mit -, deshalb erscheinen in der Mitternachtsformel beide Rechenzeichen übereinander.

Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Übungen, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter mit Matheaufgaben, die du sogar ausdrucken kannst. Übe hier online Mathe mit einer Realschullehrerin.

Nullstellen berechnen: Zwei Nullstellen (Diskriminante positiv)

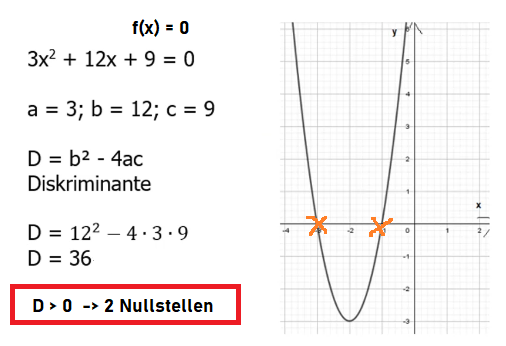
Setze zunächst die Funktionsgleichung der Parabel gleich 0, also =0. Nachdem die Nullstellen stets auf der x-Achse liegen, ist der y-Wert immer 0.
Nun kannst du a, b und c ablesen. a befindet sich immer vor dem quadratischen Glied, b vor dem Element mit x und c ist das neutrale Glied.
Mithilfe der Formel D=b²-4ac kannst du nun die Diskriminante D berechnen. Ist die Diskriminante positiv, also > 0, so weißt du, dass diese Funktion zwei Nullstellen hat.
Setze anschließend in die Mitternachtsformel ein und berechne die konkreten Koordinaten der beiden Nullstellen:

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Lerne Mathe online.

Nullstellen berechnen: Eine Nullstelle (Diskriminante =0)

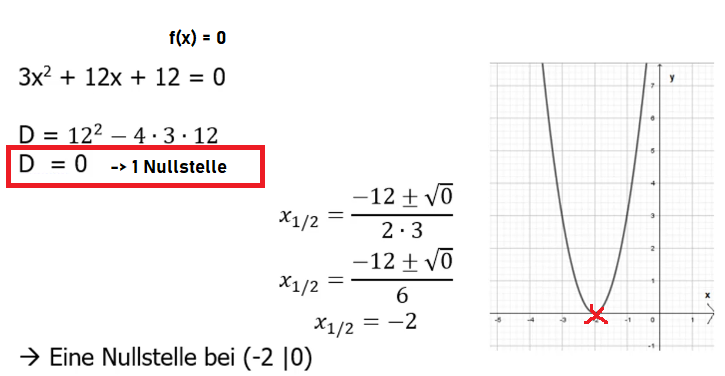
Setze zunächst die Funktionsgleichung der Parabel gleich 0, also =0. Mithilfe der Formel D=b²-4ac kannst du nun die Diskriminante D berechnen. Ist die Diskriminante 0, so weißt du, dass diese Funktion eine Nullstelle hat.
Setze anschließend in die Mitternachtsformel ein. Egal, ob du + oder – rechnest, es ergibt sich stets der gleiche Wert für die Nullstelle.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und passende Arbeitsblätter mit Matheaufgaben zum Drucken.

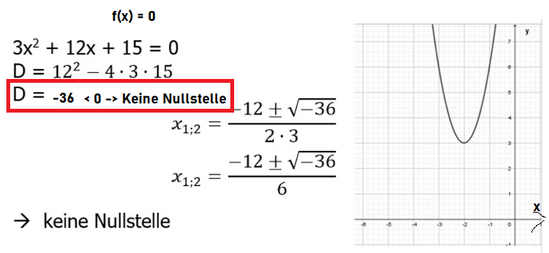
Nullstellen berechnen: Keine Nullstelle (Diskriminante negativ)

Setze zunächst die Funktionsgleichung der Parabel gleich 0, also =0. Mithilfe der Formel D=b²-4ac kannst du nun die Diskriminante D berechnen. Ist die Diskriminante negativ, so weißt du, dass diese Funktion keine Nullstelle hat.
Du braucht nun gar nicht mehr in die Mitternachtsformel einzusetzen, da diese Parabel keine Nullstelle besitzt.
Nachdem der Radikand (der Term unter der Wurzel) in diesem Fall negativ ist, kann x1 oder auch x2 nicht berechnet werden.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen und nützliche Arbeitsblätter zum Ausdrucken, um online Mathe zu üben.

Fit in die Mathe-Abschlussprüfung Mathematik (Realschule Bayern) – Prüfungsvorbereitung online (10. Klasse – 10II/III)

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.