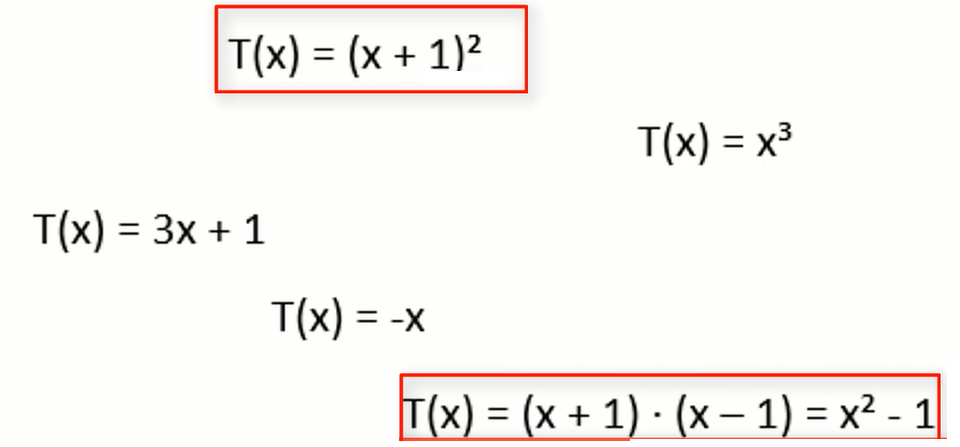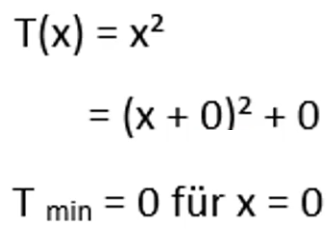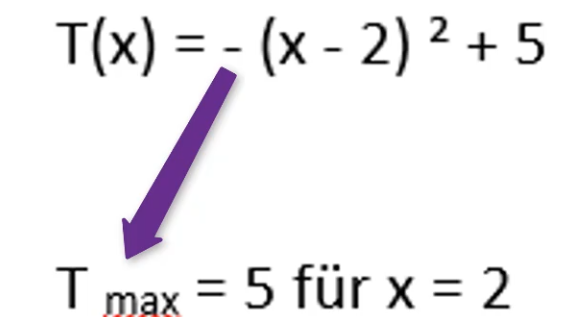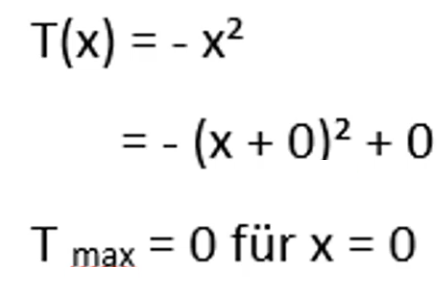Was ist ein quadratischer Term?

Ein Term ist eine sinnvolle Kombination aus Zahlen und/oder Variablen mithilfe von Rechenzeichen. In der 8. Klasse Mathe betrachtest du Terme mit dem Exponent 2 genauer. Es dürfen auch andere Variablen auftauchen, jedoch muss 2 der höchste Exponent sein. Es handelt sich dann um Quadratische Terme.
Beispiele für quadratische Terme sind: x²; x² + x; 3 – x² usw.

Extremwerte bestimmen von quadratischen Termen

Minimum (=kleinster Wert) von quadratischem Term bestimmen

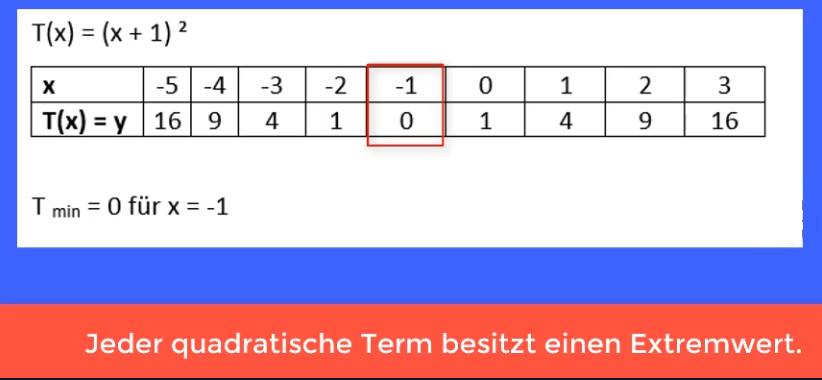
Nachem jede Variable einen Platzhalter darstellt, kannst du hierfür nacheinander Zahlen einsetzen. Hier werden für x Zahlen von -5 bis 3 eingesetzt. So entsteht eine Wertetabelle. Der für die Abschlussprüfung zugelassene Taschenrechner kann dies automatisch.
Indem du dir die berechneten y-Werte anschaust, erkennst du den Extremwert. Hier ist 0 der kleinste y-Wert, es handelt somit um ein Minimum , das für x=-1 angenommen wird.
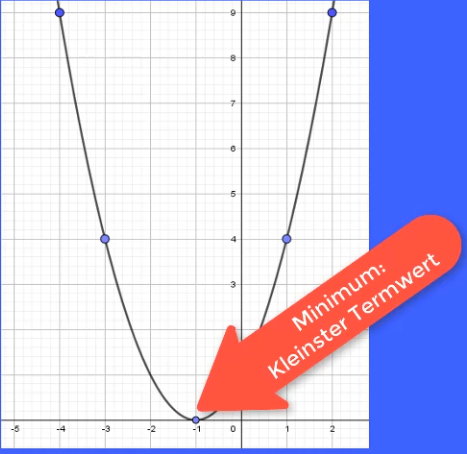
Übertrage die Zahlenpaare (xIy) in ein Koordinatensystem und du kannst auch anhand der Zeichnung erkennen, dass es sich hierbei um ein Minimum handelt.

Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von interaktiven Erklärvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu meistern.

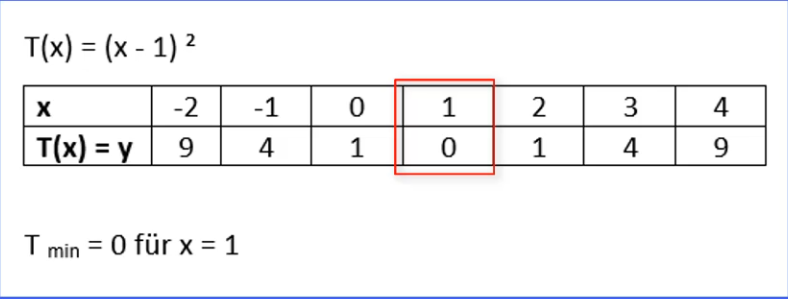
Bei diesem Beispiel wird der kleinste y-Wert 0 bei x = 1 angenommen.

Allgemein kannst du dir folgendes merken: Ist die Zahl vor dem x² positiv, so hat dieser quadratische Term als Extremwert ein Minimum.
(x – 1)² ist eine Binomische Formel (2. Binomische Formel) und lässt sich so schreiben: x² – 2x + 1. Vor dem x² steht damit eine 1. (=1x² – 2x + 1)

So ermittelst du in 3 Schritten den Extremwert (Minimum/Maximum):

Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du verständliche Mathe-Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe Mathe online mit einer Realschullehrerin.

Schritt 1: Betrachte die Zahl vor dem x² (positiv -> Minimum; negativ ->Maximum)

Schritt 2: Die Zahl nach dem quadratischem Element zeigt dir den y-Wert des Extremwerts an.

Schritt 3: Was musst du für die Variable einsetzen, damit die Klammer 0 wird? Dieser Wert ist der x-Wert des Extremwerts.

Maximum (=größter Wert) von quadratischem Term bestimmen

Schritt 1: Die Zahl vor dem x² ist negativ -> Maximum -(x²-4x+4)+5 = -x² + 4x – 4+5 =-x² +4x + 1

Schritt 2: Der y-Wert des Extremwerts beträgt +5 =5.

Schritt 3: Setzt man für x = 2 ein, so ergibt das quadratische Element 0 und der Termwert ergibt sodann 5.
Damit ergib sich der gegebene Extremwert.

Aufgaben, bei denen du nicht direkt den Extremwert mit diesen 3 Schritten ablesen kannst, musst du eine Quadratische Ergänzung durchführen. Näheres findest du hier.