Was ist ein lineares Gleichungssystem?

Ein lineares Gleichungsssystem besteht aus zwei Gleichungen (I und II), die miteinander verknüpft sind. Beide Gleichungen müssen gleichzeitig erfüllt werden, da die Verknüpfung „^“ (und zugleich) vorliegt. Mithilfe von linearen Gleichungssystemen können Schnittpunkte von zwei Funktionsgraphen (z.B. Lineare Funktionen) ermittelt werden. In der 9. Klasse Mathe der Realschule Bayern lernst du zunächst wie du dies grafisch lösen kannst und auch verschiedene rechnerische Verfahren (Gleichsetzungverfahren, Additionsverfahren und Einsetzungsverfahren).

Lineares Gleichungssystem grafisch lösen

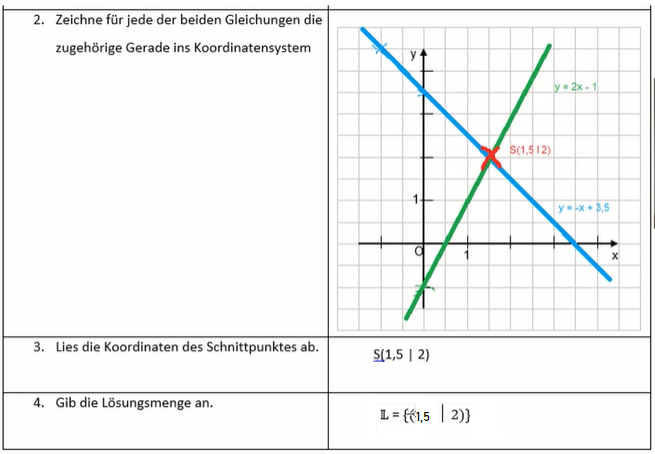
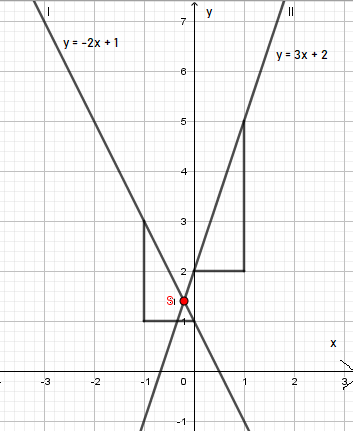
Nachdem ein lineares Gleichungssystem stets aus zwei Funktionsgleichungen besteht, ist es möglich beide Graphen in ein und dasselbe Koordinatensystem zu zeichnen und den Schnittpunkt abzulesen.
Achte darauf, dass beide Gleichungen die Form y = mx + t haben, dann kannst du den Graph der linearen Funktion direkt mithilfe eines Steigungsdreiecks einzeichnen. Wie das funktioniert, kannst du jederzeit hier nachlesen.

Wie du bereits schon vom Thema „Gleichungen„ (auch bei Bruchgleichungen) und „Ungleichungen“ kennst, brauchst du auch bei linearen Gleichungssystemen am Ende eine Lösungsmenge IL. Die Lösungsmenge wird stets mit geschweiften Klammern geschrieben und gibt die Koordinaten des Schnittpunkts an.

Lineares Gleichungssystem rechnerisch lösen

Nachdem das Grafische Lösen von linearen Gleichungssystemen zu Ungenauigkeiten führen kann, ist es wichtig, diese auch rechnerisch lösen zu können.
Hierfür gibt es verschiedene Verfahren (Gleichsetzungsverfahren, Additionsverfahren und Einsetzungsverfahren), die immer nach dem gleichen Schema ablaufen. Du kannst stets alle drei Verfahren anwenden, es gibt jedoch lineare Gleichungssysteme, die sich mit einem dieser Verfahren am Leichtesten lösen lassen. Woran du das erkennst, erfährst du, wenn du weiter liest.

Entdecke diese einzigartige Lernplattform und tauche ein in die spannende Welt des Mathematiklernens: Hier erwarten dich verständliche Mathe-Lernvideos, interaktive Übungen und praktische Arbeitsblätter mit Matheaufgaben zum direkten Ausdrucken. Übe Mathe online mit einer Realschullehrerin.

Gleichsetzungsverfahren

Beim Gleichsetzungsverfahren I =II musst du darauf achten, dass beide Funktionsgleichungen, also I und II nach der gleichen Variable aufgelöst sind. In diesem Beispiel sind bereits I und II nach y aufgelöst. Du kannst dann sofort gleichsetzen.
Ist dies nicht der Fall, musst du zunächst umformen. Wie das funktioniert, kannst du hier nachlesen.

Durch das Gleichsetzen ensteht eine Gleichung, in der nur noch eine Variable auftaucht. Die zweite Variable fällt durch das Gleichsetzen weg. Diese verbleibende Variable kann nun berechnet werden.
In diesem Beispiel gilt x = -0,2. Dieser x-Wert kann im Anschluss in I oder II eingesetzt werden. Nachdem der Schnittpunkt I und II gleichzeitig erfüllen muss, kannst du wählen. Der y-Wert ergibt hier 1,4.
Du kennst somit die Koordinaten des Schnittpunkts und kannst als Letztes die Lösungsmenge IL angeben.

Zur Kontrolle kannst du nun auch die beiden Funktionsgraphen zu I und II in ein Koordinatensystem einzeichnen. Du erkennst, dass der Schnittpunkt die Koordinaten (-0,2/1,4) hat. Die rechnerische Lösung bestätigt sich somit auch grafisch.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen, um online Mathe zu lernen. Auch kannst du nützliche Arbeitsblätter mit Matheaufgaben ausdrucken.

Einsetzungsverfahren

In der 9. Klasse lernst du in Mathematik noch ein weiteres Verfahren wie du lineare Gleichungssysteme rechnerisch lösen kannst: Das Einsetzungsverfahren.
Das Einsetzungsverfahren eignet sich besonders gut bei linearen Gleichungssystemen bei denen bereits I oder II nach einer Variable aufgelöst ist.
In diesem Beispiel siehst du, dass I y = x + 2 lautet. Hier steht die Variable y bereits auf einer Seite der Gleichung alleine.
Du setzt nun anstelle von y in II den Term x + 2 ein.
Wenn die zweite Gleichung (II) nach einer Variable aufgelöst ist, würdest du II in I einsetzen.
Berechne nun den Wert für x. Wenn die Variable x alleine steht, setzt du anstelle von x ein und berechnest sodann bei der Gleichung den Wert von y.
Hier ist dann x = 3. Diesen Wert kannst du nun in I oder II einsetzen, um y zu erhalten. Am Leichtesten ist es, wenn du x = 3 in I einsetzt, da diese Gleichung bereits nach y aufgelöst ist.
Im letzten Schritt gibt du die Lösungsmenge IL an. Die Koordinaten des Schnittpunkts lauten hier also: (3I5).

Es gibt auch Aufgaben bei denen weder I, noch II nach einer Variable aufgelöst ist.
Hier kannst du ganz frei wählen, ob du I oder II nach x oder auch nach y auflöst. Es kommen auf diese Weise ganz verschiedene Rechenwege zustande, die jedoch alle zum gleichen Ergebnis führen.
Du weißt also, wenn deine Lösungsmenge IL richtig ist, dann passt dein Weg auch.

Auf dieser Lernplattform kannst du Mathe online lernen: Du findest Mathe-Lernvideos, interaktive Übungen und Arbeitsblätter mit Matheaufgaben zum Ausdrucken.