Was ist ein Baumdiagramm?

In der 10. Klasse (Mathe Realschule) lernst du im Bereich „Daten und Zufall“ wie du mithilfe von Baumdiagrammen Zufallsexperimente veranschaulichst. Die Optik eines Baumdiagramms ähnelt mit den Verzweigungen einem Baum, daher die Bezeichnung.
Die Zweige des Baumdiagramms können mit Wahrscheinlichkeiten beschriftet werden und im Anschluss auch Wahrscheinlichkeiten von konkreten Ereignissen berechnet werden. In der Mathe-Abschlussprüfung wird oft das Erstellen eines Baumdiagramms und auch das Berechnen von Wahrscheinlichkeiten geprüft. Für die Berechnung der Wahrscheinlichkeiten können in einem Baumdiagramm sogenannte Pfadregeln verwendet werden. Zwei Pfadregeln sind sehr gängig: Multiplikationsregel und Summenregel.
Du findest hierzu Erklärungen und Beispiele.

Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Übungen, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter mit Matheaufgaben, die du sogar ausdrucken kannst. Übe Mathe online mit einer Realschullehrerin.

Beispiel für ein Baumdiagramm (Daten und Zufall):

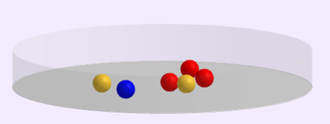
In einem Gefäß befinden sich drei rote, eine blaue und zwei gelbe Kugeln.
Nacheinander sollen zwei Kugeln gezogen werden, die Reihenfolge wird nicht berücksichtigt.

Bei diesem Beispiel handelt es sich um ein mehrstufiges Zufallsexperiment, da mehrmals nacheinander Kugeln gezogen werden. In der 10. Klasse (Mathe Realschule) lernst du wie du ein Baumdiagramm erstellen kannst:

Baumdiagramm „Ohne Zurücklegen“ (der gezogenen Kugel):

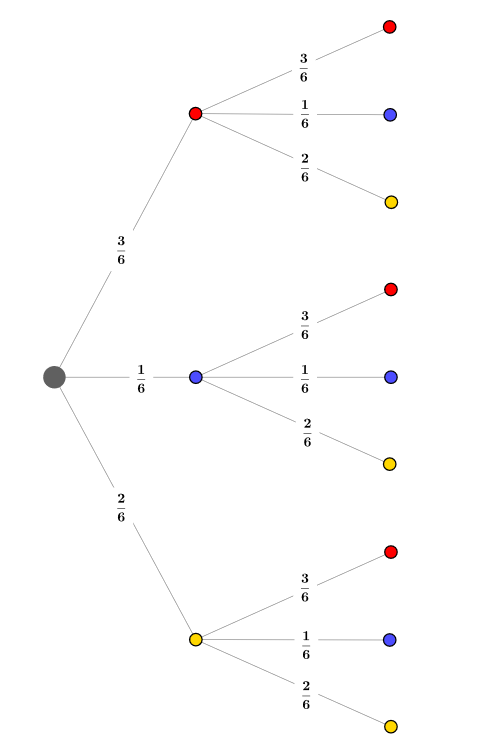
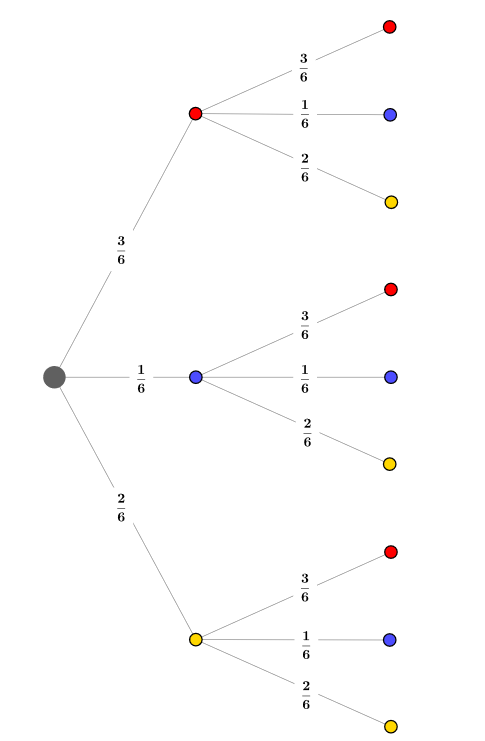
Ziehst du aus dem Gefäß eine Kugel, so kannst du eine rote, blaue oder gelbe Kugel erwischen. Nachdem es drei rote, eine blaue und zwei gelbe Kugeln im Gefäß gibt, ergeben sich verschiedene Wahrscheinlichkeiten:
Die Wahrscheinlichkeit für eine rote Kugel beträgt im ersten Zug 3/6, da drei von sechs Kugeln rot sind usw.
Alle drei Zweige insgesamt müssen die Summe 1 ergeben.
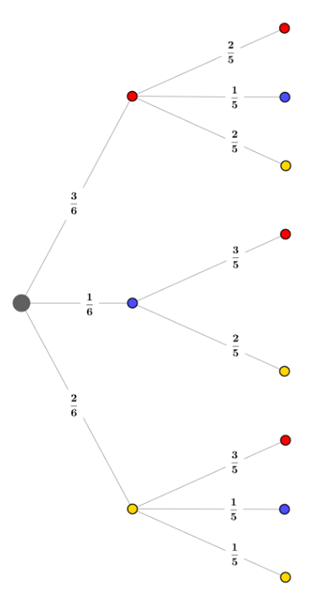
Die gezogene Kugel wird nicht mehr zurückgelegt (da „Ohne Zurücklegen“), somit ist nach dem ersten Zug eine Kugel weniger im Gefäß.
Ist die erste gezogene Kugel rot (Wahrscheinlichkeit 3/6), so sind im Anschluss noch zwei rote Kugeln von insgesamt fünf im Gefäß. Für den zweiten Zug ergibt sich deshalb eine Wahrscheinlichkeit von 2/5, dass erneut eine rote Kugel gezogen wird usw.

Willkommen auf dieser Mathe-Lernplattform: Hier erwarten dich verständliche Mathe-Lernvideos, passende Übungen und unterstützende Arbeitsblätter zum Ausdrucken.

Pfadregel im Baumdiagramm: Multiplikationsregel (Daten und Zufall)

Die Multiplikationsregel besagt, dass die Gesamtwahrscheinlichkeit eines Ereignisses, das aus mehreren unabhängigen Teilergebnissen besteht, das Produkt der Einzelwahrscheinlichkeiten dieser Teilergebnisse ist.
Angenommen, du möchtest die Wahrscheinlichkeit berechnen, dass zwei unabhängige Ereignisse A und B eintreten. Du beginnst mit einem Ast für Ereignis A und einem Ast für Ereignis B, die von einem gemeinsamen Ausgangspunkt ausgehen und multiplizierst die Wahrscheinlichkeiten.

Beispiel „Ohne Zurücklegen“: Multiplikationsregel (Pfadregel)

Berechne die Wahrscheinlichkeit für das Ereignis „zwei rote Kugeln“.

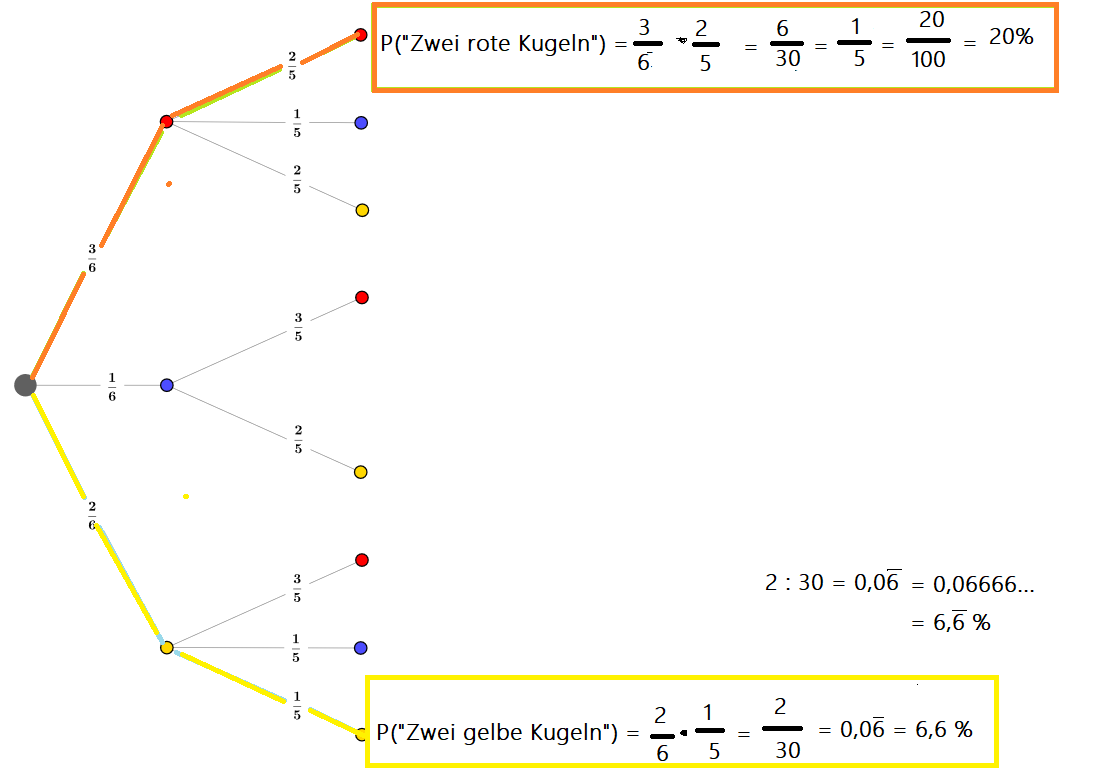
Die Wahrscheinlichkeit, dass die erste Kugel rot ist, beträgt 3/6. Nachdem auch die zweite Kugel rot sein soll, greift die Wahrscheinlichkeit von 2/5.
Du siehst im Baumdiagramm, dass du dich entlang des roten Astes bewegst, die beiden Wahrscheinlichkeiten müssen nun (aufgrund der Multiplikationsregel) multipliziert werden. Das Ergebnis ergibt damit 20 %.
Wenn du den Bruch in eine Dezimalzahl umwandelst, kannst du leichter ermitteln mit welcher Wahrscheinlichkeit (in Prozent) das Ereignis eintritt.

Berechne die Wahrscheinlichkeit für das Ereignis „zwei gelbe Kugeln“.

Hier musst du die beiden Wahrscheinlichkeiten 2/6 und 1/5 multiplizieren (Multiplikationsregel, Pfadregel). Du folgst dem gelben Ast im Baumdiagramm.
Somit ergibt sich als Ergebnis der Bruch 2/30. Wenn du 2 : 30 dividierst, ergibt sich die Dezimalzahl 0,0666…Wenn du diese mit 100 multiplizierst (um Prozent zu erhalten), weißt du, dass das Ereignis „Zwei gelbe Kugeln“ mit einer Wahrscheinlichkeit von 6,6 % eintritt.

Baumdiagramm „Mit Zurücklegen“ (der gezogenen Kugel):

Die gezogene Kugel wird nun zurückgelegt (da „Mit Zurücklegen“), somit sind nach dem ersten Zug immer noch alle Kugeln vorhanden.

Beispiel „Mit Zurücklegen“: Multiplikationsregel (Pfadregel)

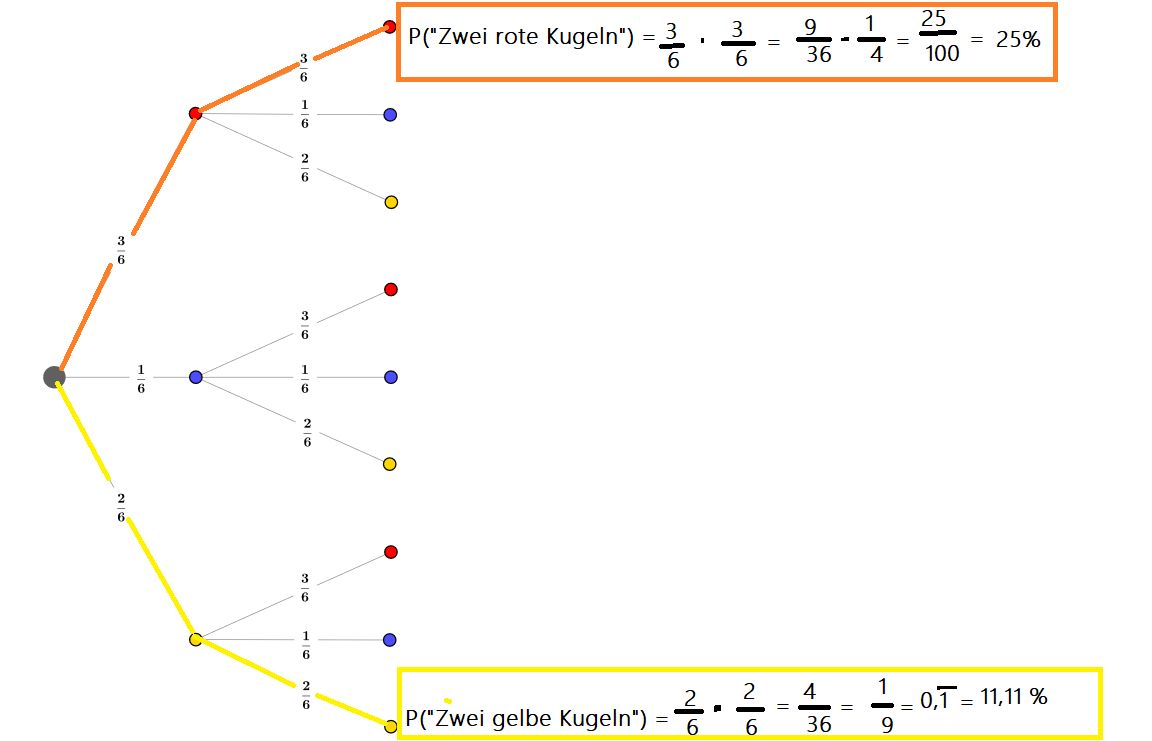
Berechne die Wahrscheinlichkeit für das Ereignis „zwei rote Kugeln“.

Die Wahrscheinlichkeit, dass die erste Kugel rot ist, beträgt 3/6. Nachdem hier die gezogene Kugel wieder ins Gefäß gelegt wird, bleibt die Wahrscheinlichkeit für das erneute Ziehen einer roten Kugel unverändert.
Du siehst im Baumdiagramm, dass du dich entlang des roten Astes bewegst, die beiden Wahrscheinlichkeiten müssen nun (aufgrund der Multiplikationsregel) multipliziert werden. Das Ergebnis ergibt damit 25 %.
Wenn du den Bruch in eine Dezimalzahl umwandelst, kannst du leichter ermitteln mit welcher Wahrscheinlichkeit (in Prozent) das Ereignis eintritt.

Berechne die Wahrscheinlichkeit für das Ereignis „zwei gelbe Kugeln“.

Hier musst du die beiden Wahrscheinlichkeiten 2/6 und 2/6 multiplizieren (Multiplikationsregel, Pfadregel). Du folgst dem gelben Ast im Baumdiagramm.

Pfadregel im Baumdiagramm: Summenregel (Daten und Zufall)

Die Summenregel besagt, dass die Wahrscheinlichkeit eines Ereignisses, das auf verschiedene Weisen eintreten kann, gleich der Summe der Wahrscheinlichkeiten dieser verschiedenen Möglichkeiten ist. Bei dieser Pfadregel musst du die Wahrscheinlichkeiten der verschiedenen Äste addieren. Bei der Multiplikationsregel hingegen bewegst du dich auf EINEM Ast, entlang der Zweige.
Hierzu gleich ein konkretes Beispiel, damit du die Pfadregel besser verstehen kannst:

Beispiel „Ohne Zurücklegen“: Summenregel (Pfadregel)

Berechne die Wahrscheinlichkeit für das Ereignis „rote und blaue Kugel“.

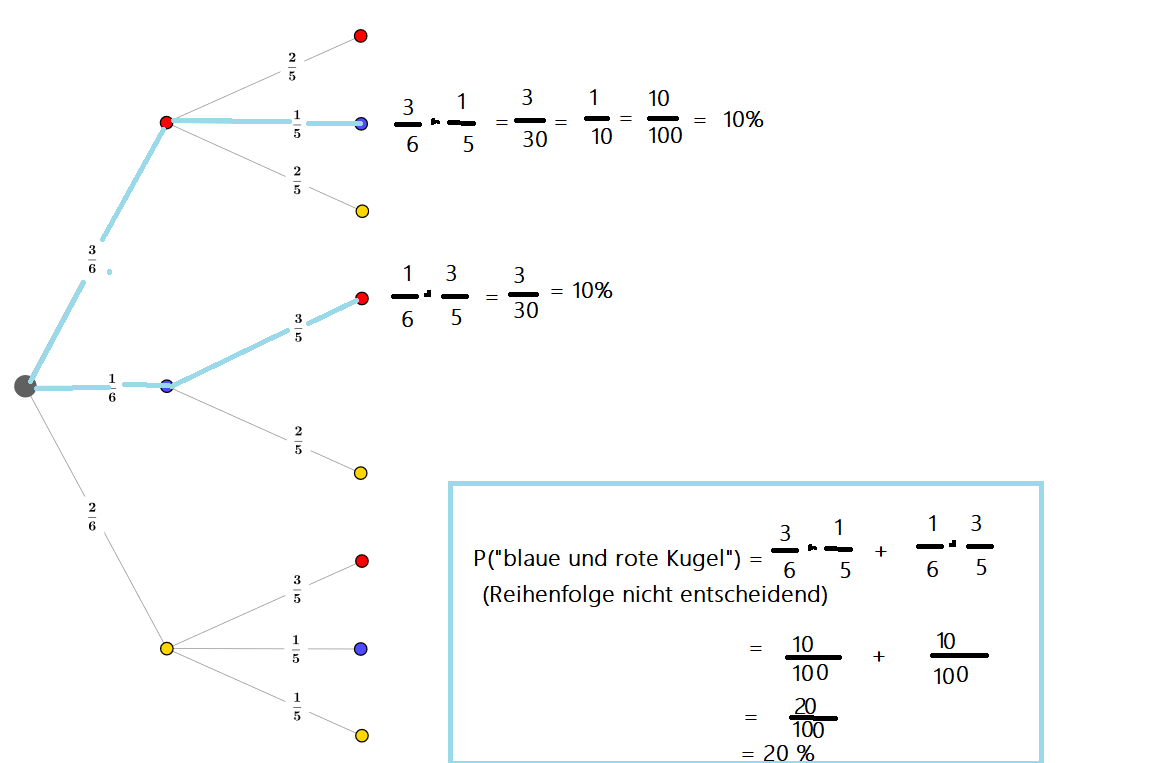
In diesem Beispiel zur Summenregel soll nun die Wahrscheinlichkeit bestimmt werden, dass „eine rote und eine blaue Kugel“ gezogen werden. Die Reihenfolge ist nicht entscheidend, deshalb kommen zwei Äste in Frage (siehe Baumdiagramm).
Die Wahrscheinlichkeit, dass zunächst eine rote und dann eine blaue Kugel gezogen wird, kannst du mithilfe der Pfadregel (Multiplikationsregel) berechnen, da du dich entlang eines Astes bewegst: 3/6 * 1/5 ergibt 1/10 und somit 100 %.
Die Wahrscheinlichkeit, dass du zunächst eine blaue und dann eine rote Kugel ziehst, ergibt ebenso 10 %.

Mithilfe der Summenregel können nun beide Äste addiert werden, sodass sich für das Ereignis insgesamt eine Wahrscheinlichkeit von 20% ergibt.
In diesem Beispiel siehst du, dass für die Zweige die Multiplikationsregel benötigt wird. Für die Berechnung der Gesamtwahrscheinlichkeit im Anschluss die Summenregel.

Beispiel „Mit Zurücklegen“: Summenregel (Pfadregel)

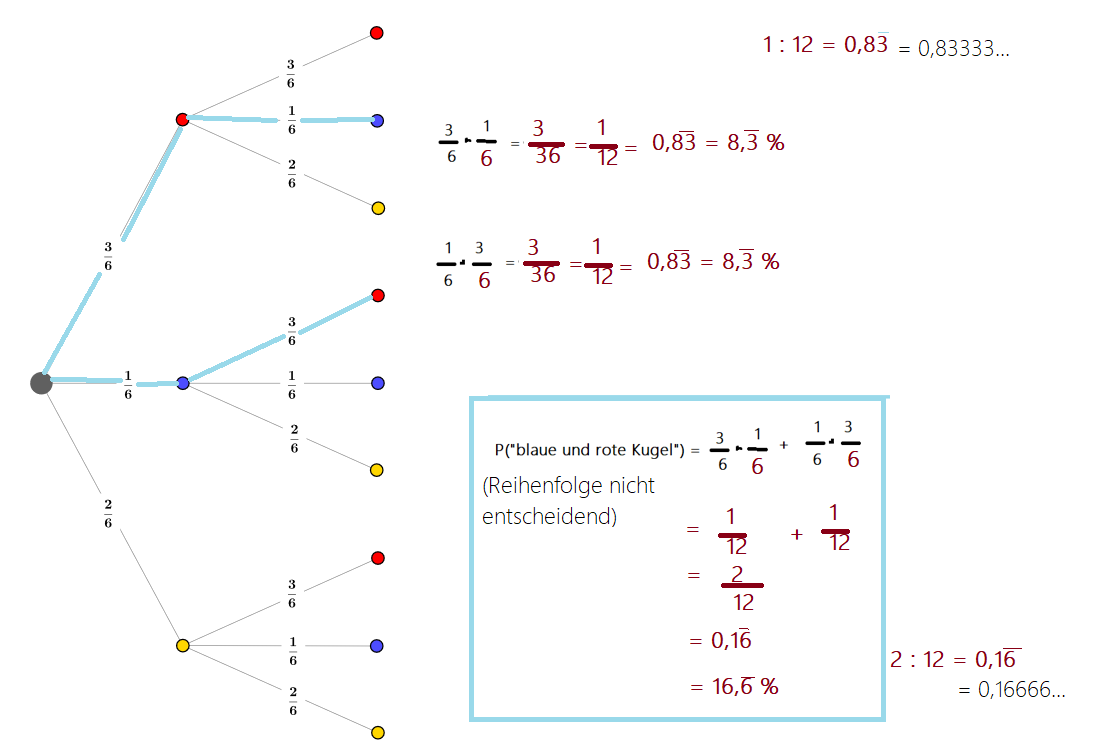
Berechne die Wahrscheinlichkeit für das Ereignis „rote und blaue Kugel“.

In diesem Beispiel siehst du, dass die Wahrscheinlichkeit der beiden Äste mit der Multiplikationsregel (Pfadregel im Baumdiagramm) berechnet werden kann. Beide Äste haben jeweils eine Wahrscheinlichkeit von 8,3 %. Um nun die Gesamt-Wahrscheinlichkeit zu ermitteln, musst du beide Äste addieren. Die Pfadregel „Summenregel“ greift und das Ergebnis lautet dann gerundet 16,67 %.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen, um online Mathe zu üben. Außerdem gibt’s hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.