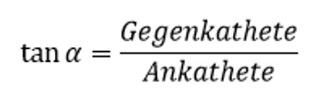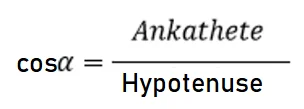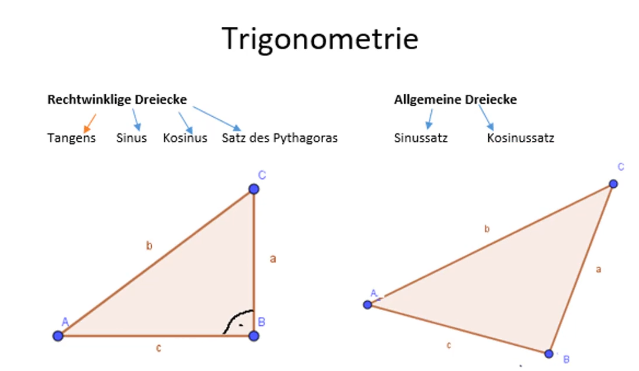
Trigonometrie ist ein Teilbereich der Geometrie, der sich mit der Berechnung von Größen (Längen oder Winkel) in Dreiecken befasst. In der Mathe-Abschlussprüfung der Realschule Bayern taucht stets mindestens eine Aufgabe dazu auf.
In der 8. Klasse Mathe der Realschule Bayern hast du gelernt Dreiecke zu zeichnen bzw. auch mit Zirkel und Lineal zu konstruieren. Längen oder Winkel wurden sodann aus der Zeichnung abgelesen, eine Berechnung ist jetzt durch diesen Bereich „Trigonometrie“ möglich.

Unterschieden werden Berechnungen in rechtwinkligen Dreiecken (mit genau einem rechten Winkel) und allgemeinen Dreiecken. Tangens, Sinus, Kosinus und auch der Satz der Pythagoras lassen sich in allen rechtwinkligen Dreiecken anwenden. Liegt jedoch kein rechtwinkliges Dreieck vor, so musst du mit dem Sinussatz oder auch Kosinussatz fehlende Größen berechnen.
Eine Erklärung im Einzelnen für Tangens, Sinus, Kosinus, Sinussatz und Kosinussatz folgt nun:

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, hilfreiche Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken. Übe hier online Mathe mit einer Realschullehrerin.

Tangens (gilt in rechtwinkligen Dreiecken)

In einem rechtwinkligen Dreieck gibt es stets zwei Katheten und eine Seite, die gegenüber vom rechten Winkel liegt, die Hypotenuse. Der Tangens beschreibt das Verhältnis von Gegenkathete zu Ankathete. Aus Sicht von alpha liegt die Seite a gegenüber, es handelt sich um die Gegenkathete. Die Seite c liegt an den Winkel alpha an und nennt sich deshalb Ankathete. Die Seite b liegt zwar auch an alpha an, liegt allerdings gegenüber vom rechten Winkel. Es ist somit die Hypotenuse und keine Kathete.

Das Ganze könnte auch aus Sicht von beta oder gamma betrachtet werden.
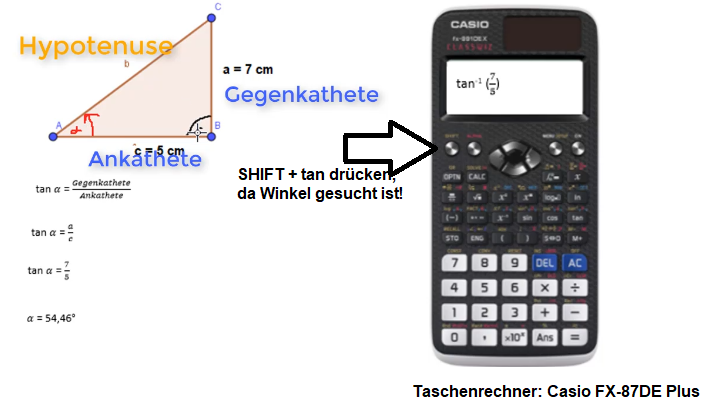
Durch Einsetzen der gegebenen Größen (hier: a = 7 cm als Gegenkathete und c = 5 cm als Ankathete) in die Formel kann nun der Winkel berechnet werden.

Merke: Immer wenn der Winkel gesucht ist, musst du SHIFT+tan drücken, der Taschenrechner zeigt tan-1 an.

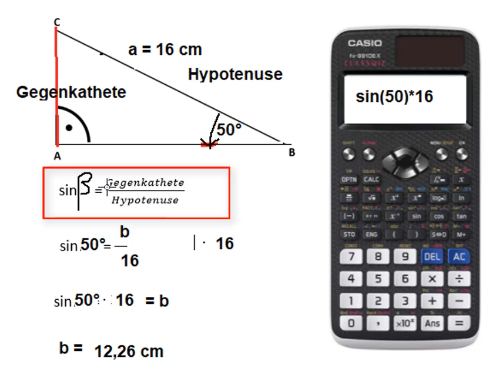
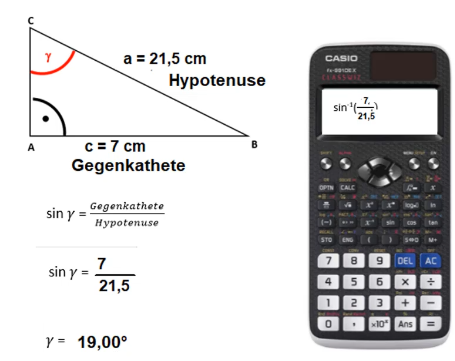
Sind Gegenkathete und Hypotenuse gegeben kann in einem rechtwinkligen Dreieck auch der fehlende Winkel berechnet werden. Nachdem im letzen Schritt sin“gamma“ dasteht, muss im Taschenrechner die Eingabe SHIFT+sin erfolgen, damit der Winkel angezeigt wird.
Achte darauf, dass im Taschenrechner die Einstellung auf „Degree“ vorliegt.

Kosinus (gilt in rechtwinkligen Dreiecken)

Der Kosinus (im Taschenrechner: cos) kommt ebenso nur in einem rechtwinkligem Dreieck zum Tragen. Das Verhältnis von Ankathete zu Hypotenuse wird als Kosinus bezeichnet.
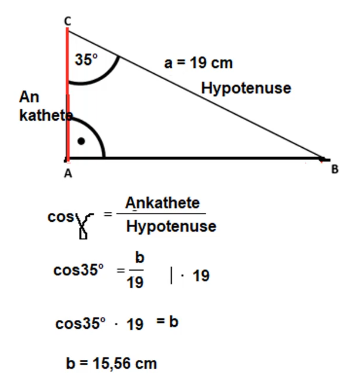
Das Beispiel zeigt, dass aus Sicht von gamma die Seite b anliegt und a die Hypotenuse darstellt. Durch Einsetzen in die Formel für den Kosinus: Ankathete /Hypotenuse kann nun die fehlende Seite b berchnet werden. SHIFT+cos wird hier nicht benötigt, da der Winkel gegeben ist.

Sinussatz (gilt in allen Dreiecken)

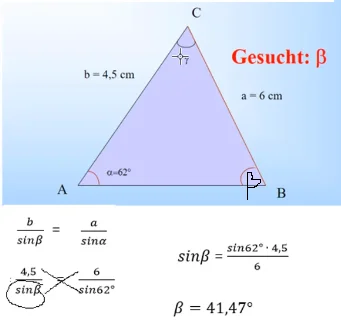
Der Sinussatz gilt in allen Dreiecken. Natürlich kann dieser dann auch in einem rechtwinkligen Dreieck verwendet werden, die Rechtwinkligkeit ist aber kein MUSS. Der Sinussatz ist eine Verhältnisgleichung/Bruchgleichung: Eine Seite verhält sich zum Sinus des gegenüberliegenden Winkels wie eine andere Seite zum Sinus ihres gegenüberliegenden Winkels. Wie du diese Verhältnisgleichung auflöst, kennst du schon von der Prozentrechnung (6. Klasse) oder Bruchgleichungen (8. Klasse): Das was gegenüber von sinß steht, landet im Nenner, die andere Verbindung wird im Zähler multipliziert.

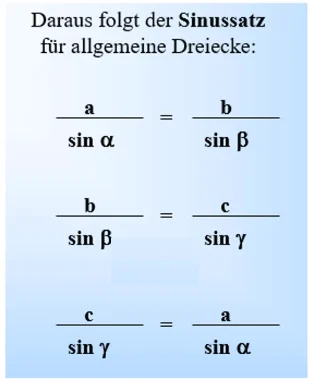
Für den Sinussatz gibt es folgende Möglichkeiten:

Beim Sinussatz können allerdings die beiden Sonderfälle eintreten: Es gibt Fälle, in denen dieser keine Lösung hat oder sogar zwei Lösungen.
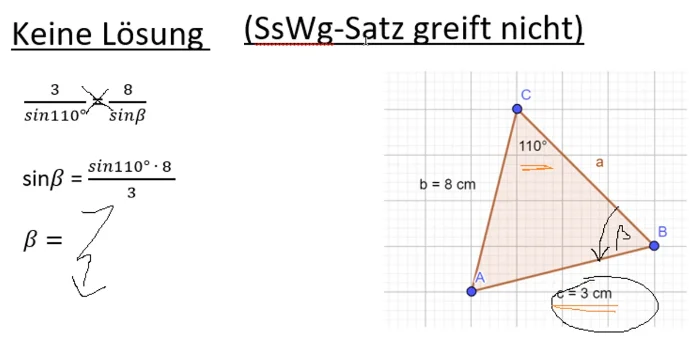
Merke: Immer wenn bei einem Dreieck der Kongruenzsatz SsWg nicht greift, tritt ein Sonderfall auf.
Sind in einem Dreieck zwei Seiten und ein Winkel gegeben, so muss die längere der beiden Seiten gegenüber vom gegebenen Winkel liegen. Ist dies nicht der Fall, so greift der SsWg-Kongruenzsatz nicht und das Dreieck existiert gar nicht (deshalb keine Lösung) oder es gibt zwei mögliche Dreiecke (deshalb zwei Lösungen).

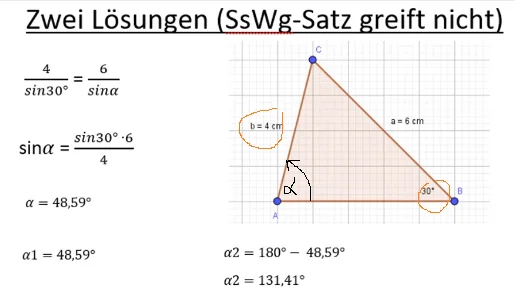
Erkennst du, dass der SsWg-Satz, so wie hier, nicht gilt, weißt du es muss ein Sonderfall vorliegen. Nachdem der Taschenrechner für alpha ein Ergebnis zeigt, weißt du, dass der Sonderfall mit zwei Lösungen vorliegen muss. Gibt es keine Lösung taucht stets ein „Mathematischer Fehler“ auf.
Die zweite Lösung bekommst du nun, indem du „180°-erste Lösung“ rechnest.

Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von verständlichen Mathe-Lernvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu meistern.

Fit in die Mathe-Abschlussprüfung Mathematik (Realschule Bayern) – Prüfungsvorbereitung online (10. Klasse – 10II/III)

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.