Gleichungen, die mindestens einen Bruchterm enthalten, werden als Bruchgleichungen oder auch Verhältnisgleichungen bezeichnet. Das bedeutet, dass nun Gleichungen gelöst werden, in denen die Variable oder mehrere Variablen im Nenner auftauchen. Wie du Gleichungen löst, weißt du bereits seit der 5. Klasse. (Wenn du dir nicht mehr sicher bist, dann klicke hier.)

So löst du Bruchgleichungen/Verhältnisgleichungen

Beispiel 1:

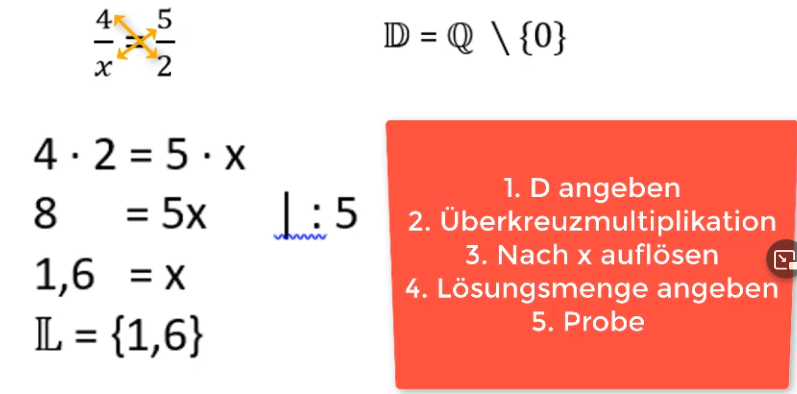
Schritt 1: Definitionsmenge angeben

Die Definitionsmenge gibt an, welche Werte für die Variable/n eingesetzt werden dürfen. Nachdem bei Bruchgleichungen die Variable mindestens einmal im Nenner auftaucht, muss beachtet werden, dass der Nenner eines Bruchs niemals 0 werden darf.
Verwende also die angegebene Grundmenge (oft IN, Z oder Q) und schließe die Werte aus, für die im Nenner eine 0 stehen würde. Beispiel: D = Q \ {0} (sprich: „Q ohne 0“) bedeutet, dass alle Zahlen aus der Zahlenmenge Q eingesetzt werden dürfen, nur die 0 nicht.

Schritt 2: Überkreuzmultiplikation („Hosenträgermethode“)

Nun geht es darum diese Bruchgleichung zu lösen. Nachdem „Hosenträger“ von hinten betrachtet auch ein X bilden, verwende ich gerne diese Eselsbrücke.
Merke: Das, was gegenüber der Variable steht, schreibst du in den Nenner, die andere Querverbindung wird im Zähler multipliziert. Es liegt eine Überkreuzmultiplikation vor.

Schritt 3: Nach Variable auflösen

Im nächsten Schritt löst du, wie du es schon von den Äquivalenzumformungen bei Gleichungen kennst, nach der Unbekannten auf. Ziel ist es, dass diese am Ende alleine auf einer Seite des „=“ steht.

Schritt 4: Lösungsmenge IL angeben

Im letzten Schritt gibt du die Lösungsmenge IL an. Das ist bei Gleichungen immer so. Hierfür prüfst du, ob der berechnete Wert für deine Variable z.B. x = 1,6 auch in der Definitionsmenge enthalten ist. Wenn dies der Fall ist, kannst du die Lösungsmenge IL = {1,6} angeben. Wäre dieser Wert nicht enthalten, liegt eine „leere Menge“ vor. Du schreibst dann: IL = { }.

Schritt 5: Probe

Um sicherzustellen, dass du wirklich richtig gerechnet hast, kannst du ganz am Ende noch eine Probe durchführen. Hierfür setzt du dein berechnetes x in die ursprüngliche Gleichung ein. Sind linke und rechte Seite der Gleichung dann identisch, weißt du, dass du korrekt gerechnet hast.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe Mathe online.

Beispiel 2:

Bruchgleichungen – Mathe 8. Klasse Realschule Bayern

In der 5. Klasse Mathematik der Realschule Bayern lernst du wie du Gleichungen mithilfe von Äquivalenzumformungen umformst. In der 6. Klasse und 7. Klasse tauchen im Lehrplan erneut Gleichungen auf, nun mit Brüchen, Dezimalzahlen und Potenzen. In der 8. Klasse Mathematik der Realschule Bayern lernst du nun wie du Gleichungen löst, wenn die Variable z.B. x im Nenner eines Bruchs steht. Diese Wissen wird beispielsweise bei der Prozentrechnung angewendet. Auch beim Vierstreckensatz in der 9. Klasse Mathematik werden Bruchgleichungen benötigt. Ebenso im Bereich Trigonometrie, konkret beim Sinussatz, werden Bruchgleichungen verwendet.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken. Übe online Mathe mit einer Realschullehrerin.