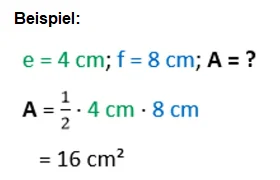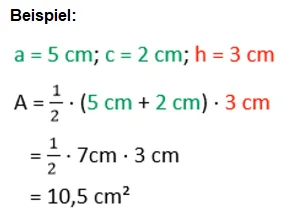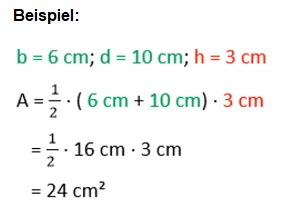Der Flächeninhalt eines Parallelogramms

Ein Viereck ist ein Parallelogramm, wenn dieses jeweils zwei parallele und gleich lange Seiten hat.

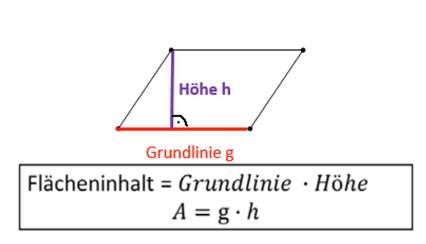
Den Flächeninhalt eines Parallelogramms berechnest du, indem du die Länge der Grundlinie g mit der Länge der Höhe h multipliziert. Es ergibt sich somit die Formel A = g * h.

Jede der vier Seiten kann als Grundlinie g verwendet werden. Die Höhe h steht jeweils senkrecht zu der gewählten Grundlinie.

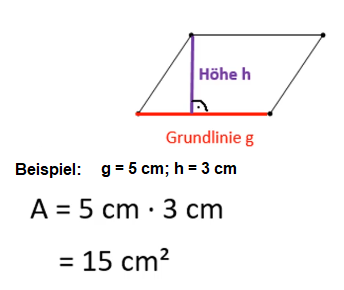
Zur Verdeutlichung ein paar Beispiele für die Berechnung des Flächeninhalts:

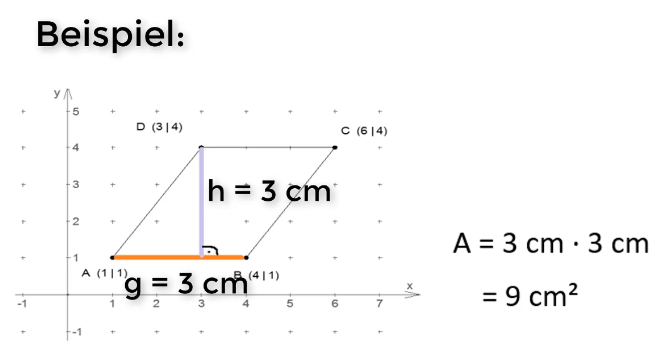
Liegt ein Parallelogramm in einem Koordinatensystem, so kann der Flächeninhalt wie folgt berechnet werden:

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter zum Ausdrucken.

Der Flächeninhalt eines Dreiecks

Du lernst in der 6. Klasse Mathematik der Realschule Bayern auch wie du den Flächeninhalt eines Dreiecks berechnen kannst.

Beachte die Besonderheit bei der Beschriftung eines Dreiecks:

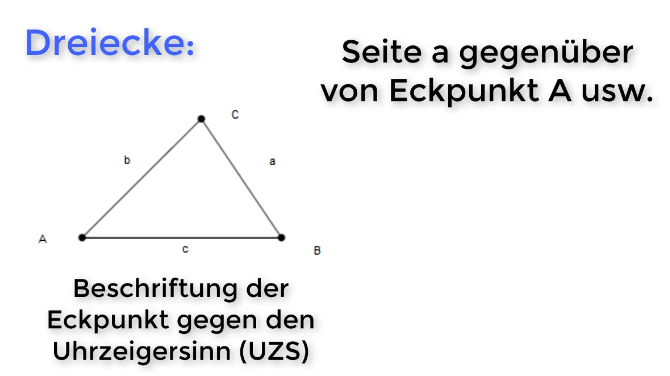
Die Seite a liegt gegenüber vom Eckpunkt A, die Seite b gegenüber des Eckpunkts B und die Seite c liegt gegenüber von C.

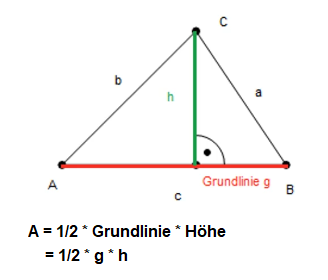
Mit dieser Formel kannst du den Flächeninhalt eines Dreiecks berechnen:

Den Flächeninhalt eines Dreiecks berechnest du, indem du die Länge der Grundlinie g mit der Länge der Höhe h multipliziert und diesen Wert halbierst bzw. mit ½ multiplizierst. Es ergibt sich somit die Formel A =½ * g * h.

Jede der drei Seiten kann als Grundlinie g verwendet werden. Die Höhe h steht jeweils senkrecht zu der gewählten Grundlinie.

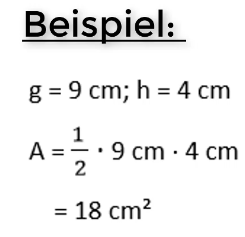
Hier nun ein Beispiel zur Flächenberechnung eines Dreiecks:

Auf dieser Lernplattform kannst du Mathe online lernen: Du findest Lernvideos, interaktive Übungen und Arbeitsblätter zum Ausdrucken.

Der Flächeninhalt eines Drachenvierecks

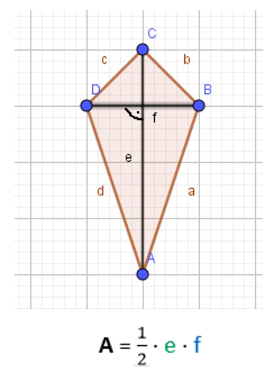
Ein Drachenviereck ist ein Viereck, bei dem die Diagonalen (mit e und f bezeichnet) senkrecht zueinander stehen.

Das Drachenviereck besitzt eine Symmetrieachse / Spiegelachse und ist damit achsensymmetrisch.

In der 6. Klasse Mathe der Realschule Bayern lernst du außerdem wie du den Flächeninhalt dieses Vierecks berechnen kannst:

Den Flächeninhalt eines Drachenvierecks berechnest du, indem du die Länge der Diagonale e mit der Länge der Diagonale f multipliziert und diesen Wert halbierst bzw. mit ½ multiplizierst. Es ergibt sich somit die Formel A =½ * e * f.

Schau dir hierzu folgendes Beispiel an:

Der Flächeninhalt einer Raute

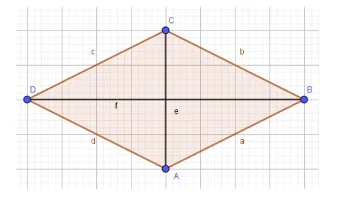
Eine Raute ist ein Viereck mit vier gleich langen Seiten, bei dem die Diagonalen (mit e und f bezeichnet) senkrecht zueinander stehen.

Die Raute besitzt zwei Symmetrieachsen / Spiegelachsen und ist damit achsensymmetrisch.

Du verwendest für die Berechnung der Fläche einer Raute die gleiche Formel wie du es bereits für das Drachenviereck gelernt hast. Auch die Berechnung der Raute wird in der 6. Klasse Mathematik der Realschule Bayern vermittelt.

Der Flächeninhalt eines Trapezes 

Ein Viereck ist ein Trapez mit zwei parallelen Seiten. Auch die Berechnung dieser geometrischen Figur lernst du in der 6. Klasse Mathematik der Realschule Bayern.

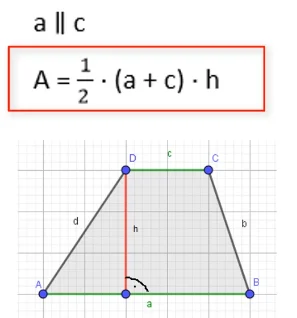
Mithilfe folgender Formel kannst du die Fläche von jedem Trapez berechnen:

Addiere die Länge der beiden parallelen Seiten, hier a und c und multipliziere mit der Länge der Höhe h und halbiere anschließend bzw. multipliziere mit ½.

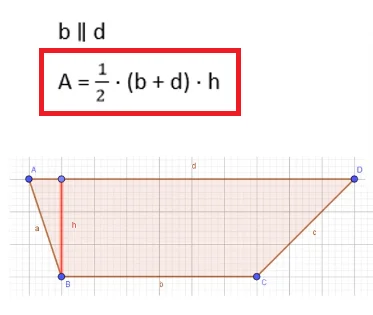
Natürlich gibt es auch Aufgaben, bei denen die Seiten b und d parallel verlaufen:

Addiere die Länge der beiden parallelen Seiten, hier b und d und multipliziere mit der Länge der Höhe h und halbiere anschließend bzw. multipliziere mit ½.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Lernvideos, spannende Übungen und praktische Arbeitsblätter zum Download.