Was bedeutet „Innenwinkelsumme“?

Grübelst du gerade, was wohl der Begriff „Innenwinkelsumme“ bedeutet? Ich kann dich gleich erlösen, du wirst sehen, das Thema kann sehr leicht sein.

Jedes Dreieck hat drei Eckpunkte. Diese werden immer gegen den Uhrzeigersinn beschriftet. An jedem Eckpunkt befindet sich ein Winkel. Dieser Winkel befindet sich innerhalb des Dreiecks, daher die Bezeichnung Innenwinkel.
Alle drei Innenwinkel addiert (deshalb Innenwinkelsumme), ergeben in Dreiecken den Wert 180°, das ist immer so.

Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von interaktiven Erklärvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu verstehen.

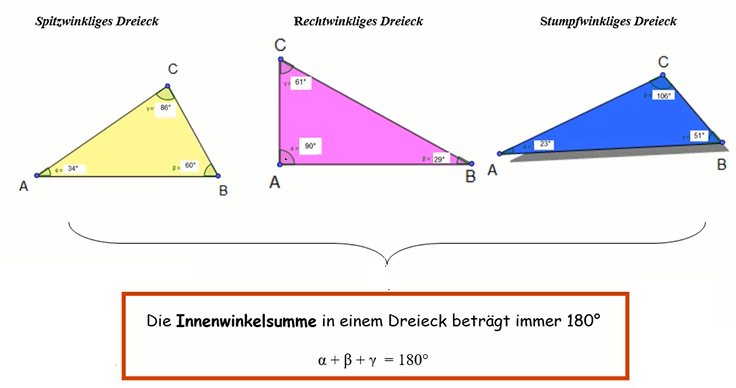
Innenwinkelsumme im spitzwinkligen, rechtwinkligen und stumpfwinkligen Dreieck

Ein Dreieck ist spitzwinklig, wenn alle drei Winkel kleiner sind als 90°. In diesem Beispiel haben die Winkel, 34°, 60° und 86°. Die Summe der drei Winkel muss immer 180° ergeben. So kannst du auch jederzeit, wenn nur zwei Winkel bekannt sind, den fehlenden dritten Winkel berechnen.

Ein Dreieck ist rechtwinklig, wenn ein rechter Winkel (=90°) vorliegt. Jetzt verstehstu du auch warum ein Dreieck nur genau einen rechten Winkel haben kann. Wären zwei rechte Winkel vorhanden, so hätten diese zusammen bereits 180°. Nachdem ein Dreieck aber immer aus drei Winkeln besteht, würde dieses Dreieck nicht existieren. In unserem Beispiel haben die einzelnen Winkel 90°, 29° und 61°. Auch in einem rechtwinkligen Dreieck besitzt die Innenwinkelsumme immer 180°.

Ein Dreieck ist stumpfwinklig, wenn ein Winkel größer als 90° ist. In unserem Beispiel hat der stumpfe Winkel 106°. Aufgrund der Innenwinkelsumme kann nur ein stumpfer Winkel dabei sin, da sonst die Innenwinkelsumme von 180° überschritten werden würde.
106°, 23° und 51° ergeben exakt 180°, so muss es immer sein, auch in allen stumpfwinkligen Dreiecken.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Erklärvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe gleich jetzt online Mathe.

Beweis für die Innenwinkelsumme im Dreieck

Wir stellen die Behauptung auf, dass in jedem Dreieck die Summe von 180° erreicht wird.
Dies muss nun bewiesen werden, damit du dich darauf verlassen kannst, dass das immer so gilt.

Zur Begründung wird nun durch den Eckpunkt C eine Parallele zur Seite AB eingezeichnet. (grüne Linien)
Entlang dieser Parallele tauchen nun Winkel auf, die zusammen 180° ergeben. Das muss so sein, da eine gerade Linie immer einen gestreckten Winkel mit 180° darstellt.

Jetzt nutzt du aus, dass du sicher weißt, dass die grüne Gerade parallel zur Seite AB verläuft. Alpha taucht nun auch an der Parallele auf, es handelt sich um einen Wechselwinkel (=Z-Winkel). Damit von der Bezeichnung ein Unterschied erkennbar ist, wird dieser alpha* genannt.
Auch Beta taucht entlang der Parallele erneut auf, auch hier handelt es sich um einen Wechselwinkel (=Z-Winkel).

Diese Vorgehensweise ist in allen Dreiecken möglich, egal ob rechtwinklig, spitzwinklig oder stumpfwinklig. Somit ist mithilfe von Wechselwinkeln bewiesen, dass die Innenwinkelsumme in allen Dreiecken 180° beträgt.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Lernvideos, passende Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken.