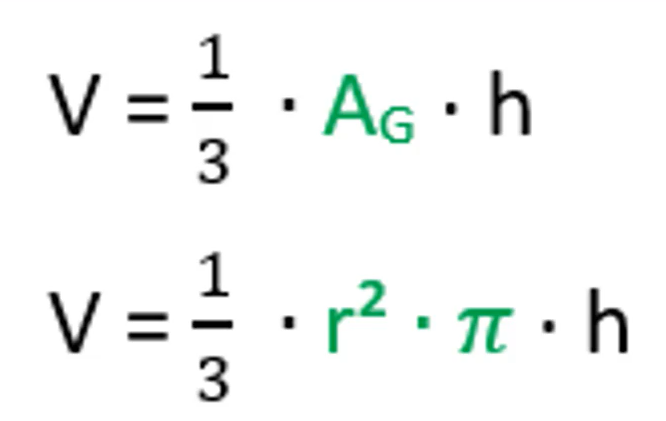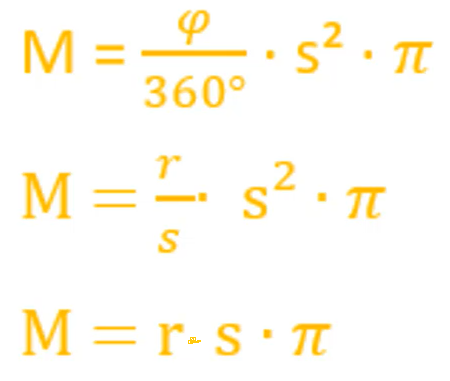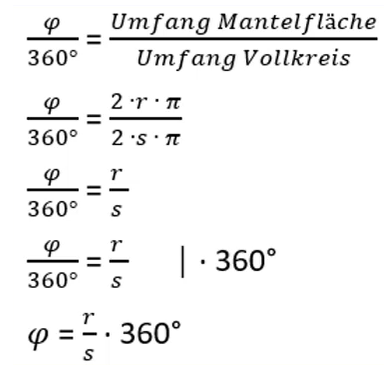Kegel als Rotationskörper (Mathe Abschlussprüfung 10 II/III Realschule)

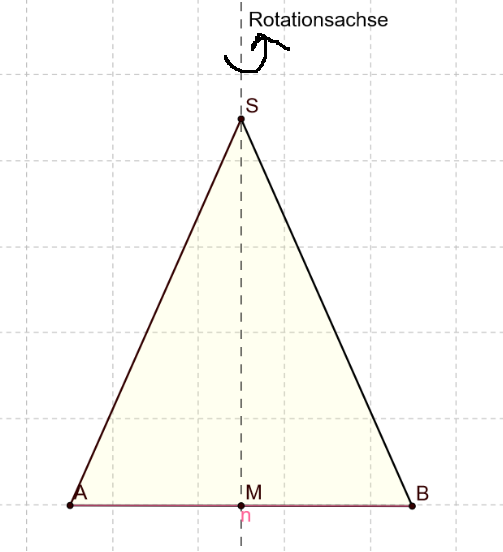
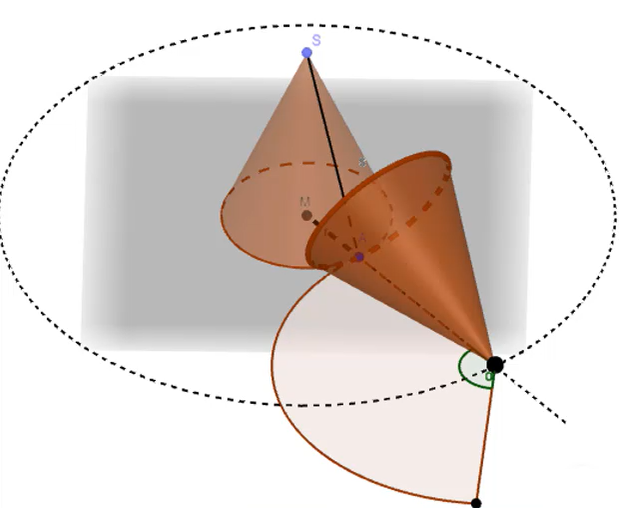
Ein Kegel entsteht durch Rotation eines Dreiecks um eine Rotationsachse (siehe Bild). Du lernst in der 10. Klasse (Mathe Realschule) weitere Rotationskörper: Kugel, Halbkugel und Zylinder.

Die Berechnung von Volumen und Oberfläche von Kegel ist ein prüfungsrelevantes Thema der Mathe-Abschlussprüfung (Realschule Bayern, 10II/III) aus dem Bereich der Raumgeometrie.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Mathe-Lernvideos, passende Übungen und nützliche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe online Mathe mit einer Realschullehrerin.

So berechnest du das Volumen eines Kegels:

Mit der Formel V = 1/3 *AG * h kannst du das Volumen jedes Kegels berechnen. Nachdem bei jedem Kegel als Grundfläche AG ein Kreis vorliegt, rechnest du hier r² * pi. Exakt drei Kegel bilden stets das Volumen eines Quaders, somit ergibt sich für das Volumen des Kegels die Formel V = 1/3 * AG * h. In der Mathe-Abschlussprüfung gilt es sehr häufig im Bereich der Raumgeometrie das Volumen des Kegels zu berechnen.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, viele Übungen und passende Arbeitsblätter mit Matheaufgaben zum Drucken. Üb jetzt gleich online Mathe.

Beispiel – Volumen eines Kegels berechnen (Radius gegeben)

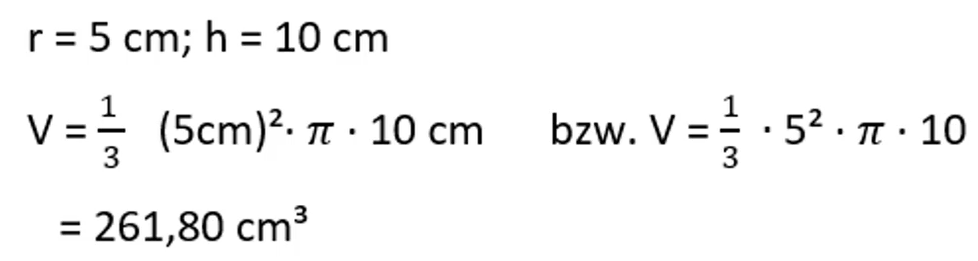
Hier in diesem Beispiel ist ein Kegel mit einem Radius r von 5 cm und einer Höhe h von 10 cm gegeben.
Setze nun in die Formel für das Volumen eines Kegels für r = 5 cm und h = 10 cm ein. Wenn du die Längeneinheit hinschreibst, musst du zwingend um (5cm)² diese Klammer setzen, damit 5 cm * 5 cm gerechnet wird. Lässt du die Klammer weg, so würde lediglich 5 cm² rauskommen.
Alternativ kannst du die Längeneinheit weglassen und nur beim Endergebnis die entsprechende Volumeneinheit angeben.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Lerne online Mathe.

So berechnest du die Oberfläche eines Kegels:

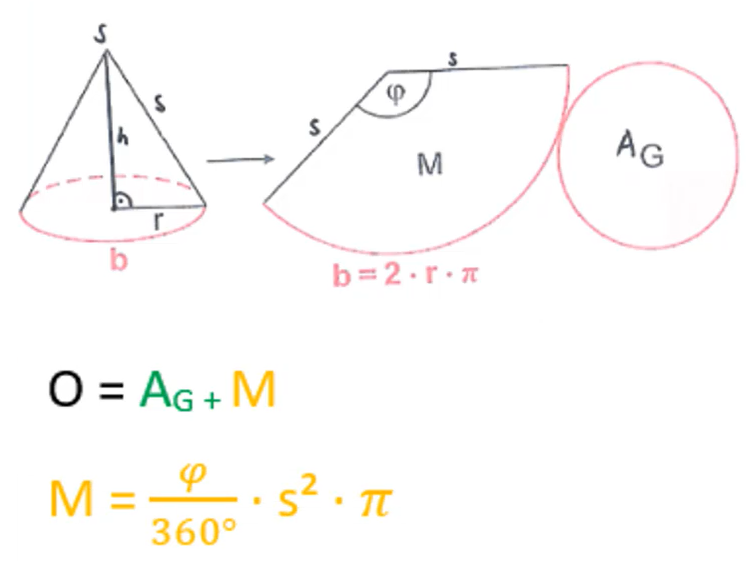
Auch das Berechnen der Oberfläche eines Kegels ist Bestandteil der Mathe-Abschlussprüfung (10II/III Realschule Bayern). Beim oberen Bild erkennst du, dass jeder Kegel aus einer Grundfläche (AG) und einem Kreissektor besteht. Die Grundfläche bildet bei jedem Kegel einen Kreis. Die Mantelfläche bildet einen Kreissektor mit dem Öffnungswinkel „phi“. (siehe Zeichnung)
Somit ergibt sich für die Oberfläche eines Kegels folgende Formel: O = AG + M.
Für die Berechnung der Mantelfläche M wird der Öffnungswinkel „Phi“ des Kreissektors und s benötigt.
Alternativ kannst du auch eine der beiden anderen Formeln für die Berechnung der Mantelfläche M verwenden, je nachdem, ob du „phi“ und s bzw. den Radius und s kennst:

Natürlich ist es auch möglich den Öffnungswinkel „phi“ zu ermitteln, wenn dieser nicht gegeben ist. Wenn du den Radius r und s kennst, kannst du phi berechnen, indem du r /s * 360° rechnest.
Die Herleitung dieser Formel siehst du in den einzelnen Schritten aufgeführt:

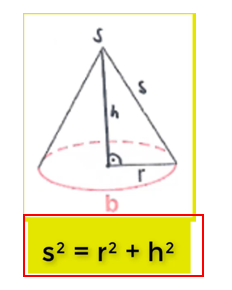
Nachdem der Radius des Kegels r und die Höhe des Kegels h rechtwinklig zueinander stehen, kann hier die Seite s mithilfe vom Satz des Pythagoras berechnet werden.

Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du anschauliche Mathe-Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Beispiel – Oberfläche eines Kegels berechnen (Radius gegeben)

Entdecke diese einzigartige Lernplattform und tauche ein in die spannende Welt des Mathematiklernens: Hier erwarten dich verständliche Mathe-Lernvideos, interaktive Übungen und praktische Arbeitsblätter mit Matheaufgaben zum direkten Ausdrucken. Lerne Mathe mit einer Realschullehrerin.

Fit in die Mathe-Abschlussprüfung Mathematik (Realschule Bayern) – Prüfungsvorbereitung online (10. Klasse – 10II/III)

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.