Winkel messen und zeichnen – Lernvideos und Aufgaben (Mathe 5. Klasse)
Hier geht’s zu Mathe-Videos & Aufgaben
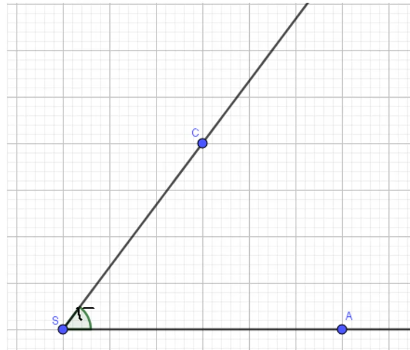
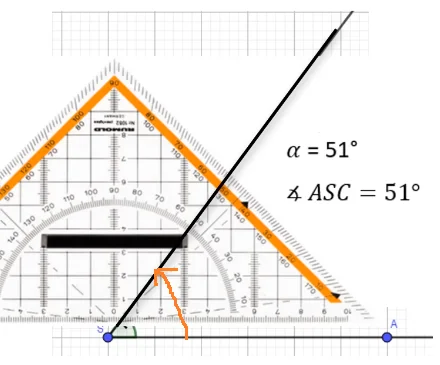
Beispiel 1: Winkel messen und zeichnen (Spitzer Winkel)
Leg das Geodreieck mit dem Nullpunkt auf den Scheitel des Winkels. Die Kante des Geodreiecks legst du entlang des einen Schenkels. Den zweiten Schenkel benötigst du nun, um am Geodreieck abzulesen wie groß der Winkel ist.
Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter zum Ausdrucken.
Hier geht’s zu Mathe-Videos & Aufgaben
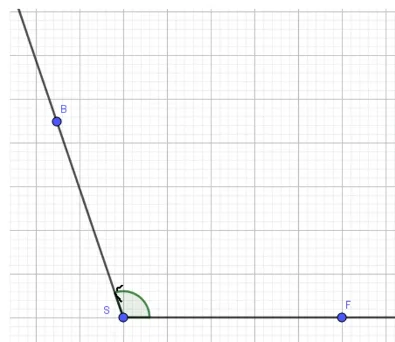
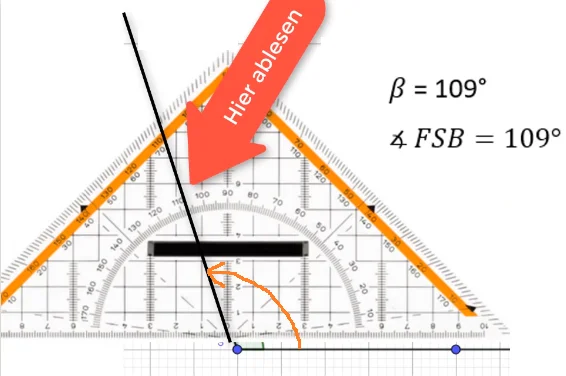
Beispiel 2: Winkel messen und zeichnen (Stumpfer Winkel)
Auf dieser Lernplattform kannst du Mathe online lernen: Du findest Lernvideos, interaktive Übungen und Arbeitsblätter zum Ausdrucken.
Hier geht’s zu Mathe-Videos & Aufgaben
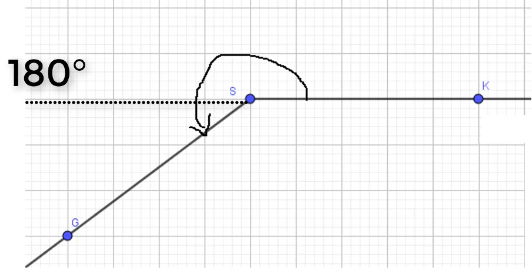
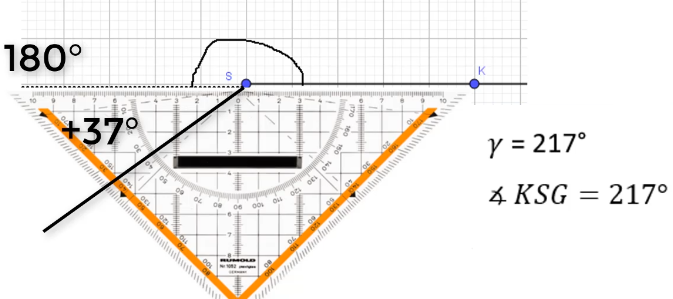
Beispiel 3: Winkel messen und zeichnen (Überstumpfer Winkel)
Auf dieser Lernplattform entdeckst du die Welt der Mathematik online: Hier findest du inspirierende Lernvideos, herausfordernde interaktive Übungen und nützliche Arbeitsblätter, die du bequem ausdrucken kannst.
Hier geht’s zu Mathe-Videos & Aufgaben
In der 5. Klasse Mathe der Realschule lernst du wie du Winkel misst und zeichnest.
Ein Winkel besteht immer aus zwei Schenkeln (Halbgeraden) und einem Scheitelpunkt. In diesem Beispiel ist der Punkt S der Scheitelpunkt. Die Schenkel bilden die Halbgeraden [SA und [SC. Beachte, dass Winkel immer gegen den Uhrzeigersinn beschriftet werden!
Für die Bezeichnung von Winkeln werden häufig die Buchstaben aus dem griechischen Alphabet verwendet. Alternativ kann die Bezeichnung von Winkeln auch mithilfe von 3 Punkten erfolgen z.B. ASC. Der mittlere Punkt, hier S, stellt immer den Scheitelpunkt dar.
Im Lehrplan Mathematik der 5. Klasse (Realschule Bayern) lernst du wie du Winkel zeichnest und auch misst.
Alle Winkel, die kleiner als 90° sind, werden als spitze Winkel benannt. Wie du spitze Winkel misst oder auch zeichnest, siehst du in Beispiel 1.
Winkel, die größer als 90° und kleiner als 180° sind, heißen stumpfe Winkel. Wie du stumpfe Winkel misst oder auch zeichnest, siehst du in Beispiel 2.
Winkel zwischen 180° (gestrecker Winkel) und 360° (Vollwinkel) heißen überstumpfe Winkel. Wie du überstumpfe Winkel misst oder auch zeichnest, siehst du in Beispiel 3. Hier ist es oft sehr hilfreich, wenn du die 180°-Linie (gestrichelt) einträgst und dann den noch fehlenden Winkel nach unten hin anträgst.
Entdecke diese Lernplattform und lerne Mathe online: Tauche ein in interaktive Übungen, schaue inspirierende Lernvideos und drucke Arbeitsblätter zum Üben aus.
Hier geht’s zu Mathe-Videos & Aufgaben
Winkel im Lehrplan PLUS der Realschule Bayern
In der 5. Klasse Mathematik der Realschule Bayern lernst du wie du Winkel benennst, misst und zeichnest.
Dieses Wissen wird in der 5. Klasse gleich erweitert und angewendet bei Neben- und Scheitelwinkeln.
In der 6. Klasse (Mathematik der Realschule Bayern) tauchen Winkel bei der Achsenspiegelung (Diese ist beispielsweise immer winkeltreu) auf.
Auch für die Zeichnung bzw. Konstruktion der Winkelhalbierenden werden Winkel benötigt. Wie das funktioniert, lernst auch in der 6. Klasse Mathematik.
Entdecke diese einzigartige Lernplattform und tauche ein in die spannende Welt des Mathematiklernens: Hier erwarten dich verständliche Lernvideos, interaktive Übungen und praktische Arbeitsblätter zum direkten Ausdrucken.
Hier geht’s zu Mathe-Videos & Aufgaben