In der 7. Klasse Mathe der Realschule lernst du die Indirekte Proportionalität. Dies ist Bestandteil des LehrplanPLUS, unabhängig von der Wahl deiner Wahlpflichtfächergruppe. In der 6. Klasse hast du bereits die Zuordnung der direkten Proportionalität gelernt, nun in der 7. Klasse wird die indirekte Proportionalität ergänzt.

Hier in diesem Beispiel liegt eine indirekt proportionale Zuordnung vor:
Verdoppelt sich die Anzahl der Arbeiter, so benötigen diese nur die Hälfte an Zeit.
Verdreifacht  sich die Anzahl der Arbeiter, so benötigen diese nur ein Dritter der Arbeitszeit.

Während x mit einem Faktor multipliziert wird, muss y gleichzeitig mit dem gleichen Wert dividiert werden. Dieser Zusammenhang liegt immer bei einer indirekten Proportionalität vor.

Analog gilt auch, die Hälfte der Arbeiter (x wird halbiert), benötigen die Doppelte Arbeitszeit (y wird verdoppelt).

Bei der direkten Proportionalität werden x und y mit demselben Faktor multipliziert. Es kann auch sein, dass x und y mit demselben Divisor dividiert werden. Entscheidend ist, dass mit x und y dasselbe passiert.

Bei der indirekten Proportionalität hingegen passiert mit x und y jeweils das Gegenteilige.
Wird x multipliziert, so wird y dividiert.
Wird x dividiert, so wird y multipliziert.

Produktgleichheit bei einer indirekten Proportionalität (Mathe 7. Klasse)

Die x- und y-Werte aus der Wertetabelle können nun als Zahlenpaare (xIy) geschrieben werden.

Rechnest du y * x, so stellst du bei einer indirekten Proportionalität fest, dass sich hierbei stets das gleiche Produkt ergibt.
In diesem Beispiel ergibt sich für den gemeinsamen Produktwert 180.
Denn:
10 * 18 = 180
20 * 9 = 180
30 * 6 = 180
usw.

Bei Aufgaben in Mathematik zur indirekten Proportionalität ist es an der Realschule Bayern sehr häufig so, dass Lücken in Wertetabellen gefüllt oder Zahlenpaare auf indirekte Proportionalität geprüft bzw ergänzt werden sollen.

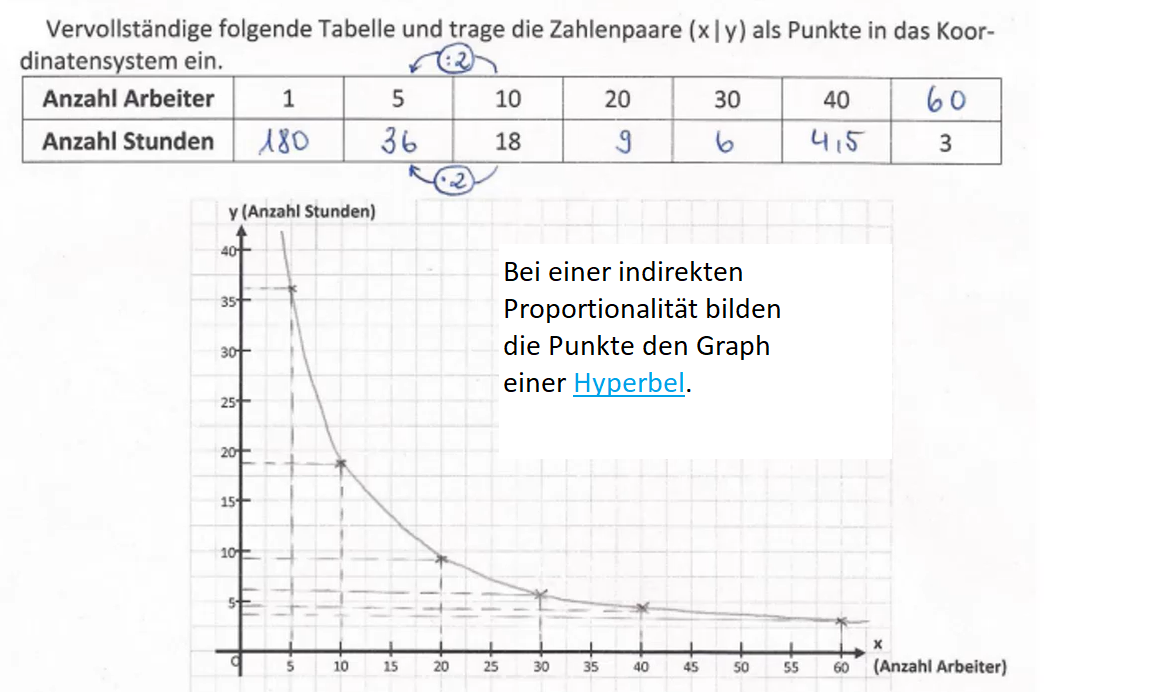
Hyperbel als Graph bei einer indirekten Proportionalität

Die Zahlenpaare (xIy) stellen Punkte im Koordinatensystem dar. Überträgst du diese nun in ein Koordinatensystem und verbindest sie zu einem Graph, so entsteht eine Hyperbel. Immer wenn eine indirekte Proportionalität vorliegt, muss eine Hyperbel entstehen. Umgekehrt gilt auch: Liegt eine Hyperbel als Graph vor, so handelt es sich um eine indirekte Proportionalität.

Bei einer direkten Proportionalität (Mathe 6. Klasse) hingegen ist als Graph eine Ursprungshalbgerade entstanden.
Erkennst du, dass bei einer Zuordnung weder eine Ursprungshalbgerade, noch eine Hyperbel ensteht, handelt es sich um keine direkte oder indirekte Zuordnung. Es gibt auch Zuordnungen, die weder noch sind.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, passende Matheaufgaben und praktische Arbeitsblätter zum Drucken.

Indirekte Proportionalität und Beispiele für die Anwendung

Das Thema „Indirekte Proportionalität“ ist im Lehrplan Mathematik der Realschule Bayern in der 7. Klasse verankert.  Das Thema gehört in den roten Themenbereich „Funktionaler Zusammenhang“. Bereits in der 6. Klasse hast du die Zuordnung der direkten Proportionalität gelernt, darauf baut jetzt in der 7. Klasse die Indirekte Proportionalität auf.
In 8I bzw. 9II/III wird das Thema „Direkte Proportionalität“ erneut aufgegriffen und hin zur „Linearen Funktion“ erweitert.

Im Alltag findest du zahlreiche Beispiele für eine indirekt proportionale Zuordnung:
– Für doppelt so viel Pferde, reicht der Futtervorrat nur halb so lang
– Die doppelte Zahl an Wasserpumpen, benötigt nur die Hälfte an Zeit
usw.

Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Matheaufgaben, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter, die du sogar ausdrucken kannst.