Was ist eine Winkelhalbierende?

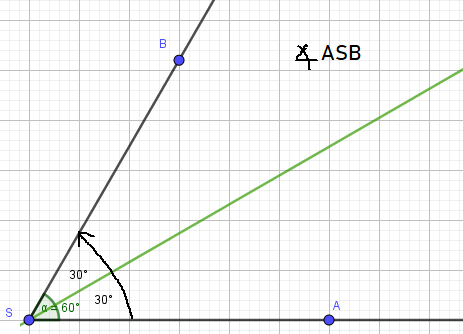
Eine Winkelhalbierende teilt einen beliebigen Winkel in zwei gleich große Hälften. Nachdem die Winkelhalbierende die Symmetrieachse bzw. Spiegelachse eine Winkels ist, taucht diese im Themengebiet „Achsenspiegelung“ taucht in der 6. Klasse Mathematik der Realschule Bayern auf. In diesem Zusammenhang lernst du auch wie du auch eine Mittelsenkrechte zeichnest und konstruierst.

Entdecke diese Lernplattform und übe online Mathematik: Tauche ein in interaktive Aufgaben, schaue inspirierende Mathe-Lernvideos und drucke Arbeitsblätter mit Mathe-Aufgaben zum Üben aus.

Welche Eigenschaften hat eine Winkelhalbierende?

Alle Punkte, die auf der Winkelhalbierende liegen, haben eine gemeinsame Eigenschaft: Sie haben alle den gleichen Abstand von den beiden Schenkeln. Umgekehrt gilt ebenso, dass alle Punkte, die von den beiden Schenkeln den gleichen Abstand haben, auf der Winkelhalbierende liegen.

Wie zeichnest du eine Winkelhalbierende?
Gehe so vor:

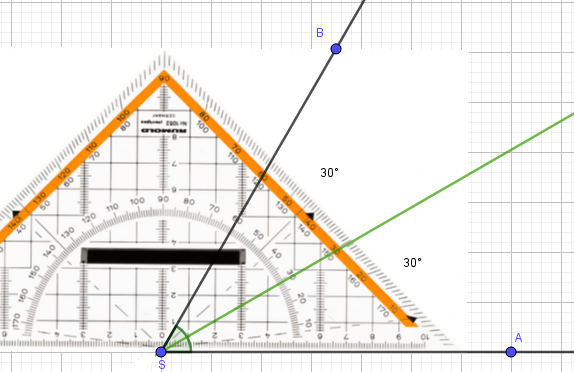
Möchtest du eine Winkelhalbierende zeichnen, so benötigt du am Besten ein Geodreieck und einen Bleistift.
Schritt 1: Lege das Geodreieck mit dem Nullpunkt an den Scheitelpunkt des Winkels. Die Geodreieckkante liegt entlang eines Schenkels. Miss anschließend die Größe des Winkels.

Schritt 2: Lies am Geodreick ab, wo sich die Hälfte befindet. (Hier: 30°)

Schritt 3: Verbinde nun den Scheitelpunkt (Spitze des Winkels mit dem markierten Punkt. (siehe Zeichnung oben)

FERTIG!

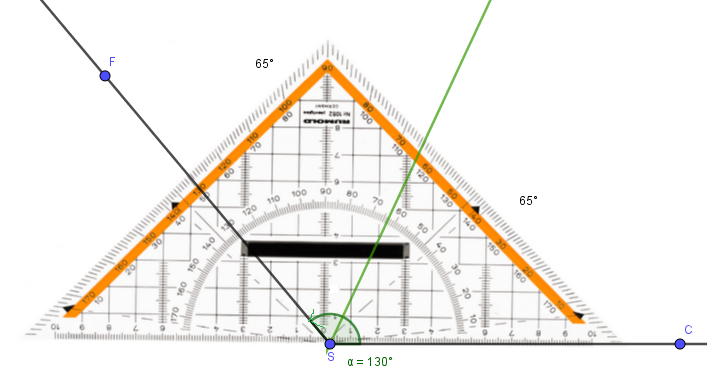
Auch bei stumpfen Winkel (größer als 90°, jedoch kleiner als 180°) oder überstumpfen Winkel (größer als 180°) funktioniert diese Vorgehensweise.

Hier findest du ein Beispiel für den stumpfen 130°-Winkel:

Winkelhalbierende konstruieren (mit Zirkel und Lineal): Schritt für Schritt

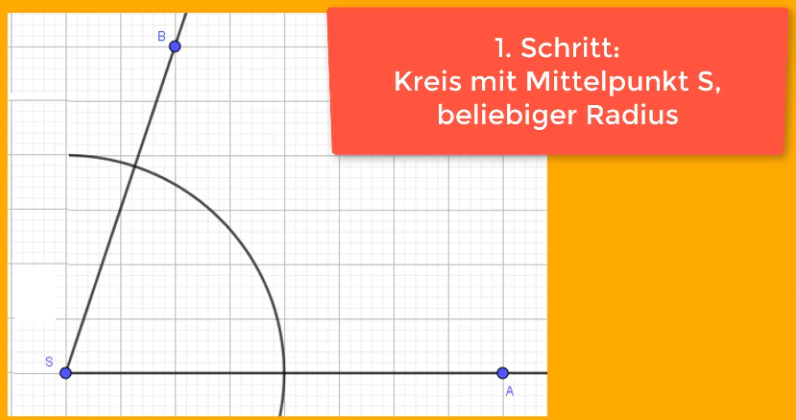
Im ersten Schritt, wenn du eine Winkelhalbierende konstruieren möchtest, stichst du mit dem Zirkel in den Scheitelpunkt des Winkels ein. Wähle einen beliebigen Kreisradius.

Im zweiten Schritt benötigst du für die weitere Konstruktion der Winkelhalbierenden nun die beiden Schnittpunkte des Kreises mit den Schenkeln.
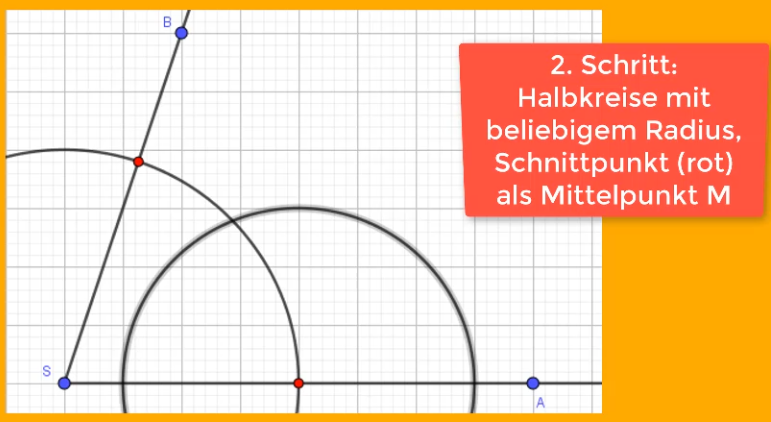
Stich mit dem Zirkel nun in einen der beiden Schnittpunkte ein, wähle einen beliebigen Radius (kann sich vom Radius von Schritt 1 unterscheiden) und zeichne einen Halbkreis.
Anschließend behältst du den gleichen Radius bei und stichst in den zweiten Schnittpunkt ein.
Die beiden Halbkreise müssen sich schneiden, sonst hast du den Radius zu klein gewählt.

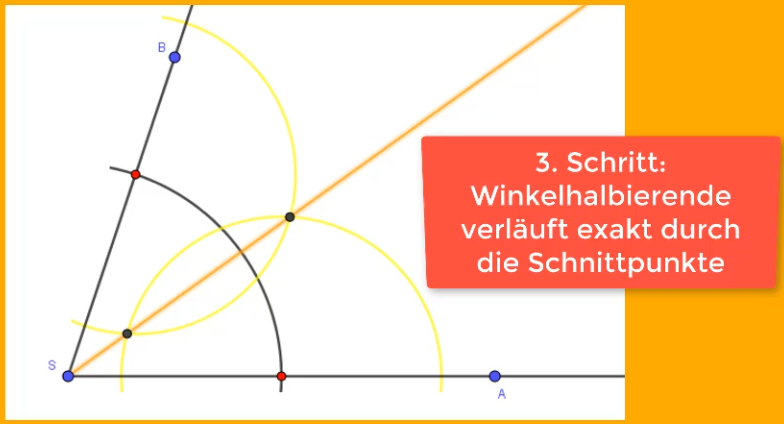
Im dritten und letzten Schritt der Winkelhalbierenden-Konstruktion verbindest du nun den Scheitelpunkt des Winkels mit dem Schnittpunkt der Halbkreise.
Die nun entstandene Halbgerade ist eine Winkelhalbierende. Die Zirkelspuren müssen sichtbar sein, wenn du diese konstruieren solltest.

Auf dieser Lernplattform kannst du Mathe online üben: Du findest Mathe-Lernvideos, interaktive Aufgaben und Arbeitsblätter zum Ausdrucken.