Jeder quadratische Term besitzt einen Extremwert (Minimum oder Maximum). Ist der höchste Exponent, der auftaucht 2, so handelt es sich um einen quadratischen Term. In der 8. Klasse Mathe der Realschule Bayern lernst du wie du einen quadratischen Term so umwandeln kannst, dass du am Ende die Art (Maximum oder Minimum) und die Lage des Extremwerts ablesen kannst, z.B. Tmin = -3 für x = 4.

In 10 II/III bzw. 9 I Mathe der Realschule Bayern brauchst du die quadratische Ergänzung auch wieder, um die Koordinaten des Scheitels einer Parabel zu berechnen.

Quadratische Ergänzung – Wie geht das?

Wenn du nicht genau weißt, wie du von (x-4)² – 3 auf Tmin = -3 für x = 4 kommst, dann klicke hier.

Dir liegt ein Term in der Form ax² + bx + c vor, hier: 1x² – 8x + 13.

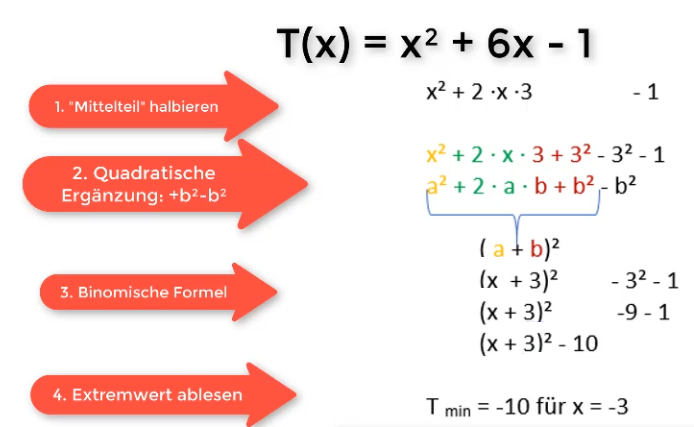
• Schritt 1: Halbiere die Zahl, die vor dem x steht.
  -8 : 2 = -4, deshalb -8x = -2*x*4
• Schritt 2:Quadratische Ergänzung: +4² – 4²
  Es soll nun eine Binomische Formel entstehen, damit wir in eine kompakte Klammer umwandeln könnnen.

a² + 2*a*b + b² = (a + b)²   – Erste Binomische Formel
a² – 2*a*b+b² = (a – b)²    – Zweite Binomische Formel

• Schritt 3: Binomische Formel anwenden (hier: Zweite Binomische Formel)

x² – 2 * x * 4 + 4² = (x – 4)²
x² – 2 * x * 4 + 4² – 4²= (x – 4)² – 4²

Nachdem 4² einfach hinzugefügt wurde, damit die Erste oder Zweite Binomische Formel greift, muss nun, damit die Rechnung richtig bleibt, 4² auch gleich wieder subtrahiert werden. (=Quadratische Ergänzung)

• Schritt 4: Alles was nach der Klammer steht noch zusammenfassen: -4² + 13 = -16 + 13 = -3
• Schritt 5: Extremwert ablesen und angeben

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe Mathe online mit einer Realschullehrerin.

Quadratische Ergänzung – kompakt:

Quadratische Ergänzung: Weitere Beispiele

Willkommen auf dieser Lernplattform für Mathe von einer Realschullehrerin: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken. Übe hier online Mathe.