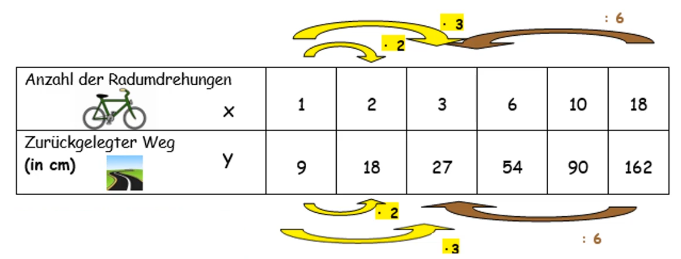
Hier in diesem Beispiel liegt eine direkt proportionale Zuordnung vor:
Dreht sich das Rad 1x, so legt das Spielzeugrad einen Weg von 9 cm zurück.
Dreht sich das Rad 2x, so beträgt der Weg 18 cm.
Verdreifacht sich die Anzahl der Radumdrehungen, so verdreifacht sich auch der zurückgelegte Weg usw.
Umgekehrt gilt ebenso: Sechstelt sich der zurückgelegte Weg, so sechstelt sich auch die Anzahl der Radumdrehungen usw.

Dieser Zusammenhang besteht immer bei einer Direkten Proportionalität.
Multiplizierst du x, so musst du y mit demselben Faktor multiplizieren. Ist dies nicht der Fall, so liegt keine direkte Proportionalität vor.
Dividierst du y, so musst du diese Division ebenso bei x durchführen.

Quotientengleichheit bei einer direkten Proportionalität

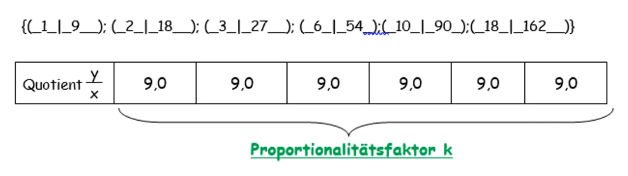
Die x- und y-Werte aus der Wertetabelle können nun als Zahlenpaare (xIy) geschrieben werden.

Rechnest du y : x, so stellst du bei einer direkten Proportionalität fest, dass sich hierbei stets der gleiche Quotient ergibt. Dieser gleiche Quotientenwert wird als Proportionalitätsfaktor k bezeichnet.
In diesem Beispiel ergibt sich für k = 9.
Denn:
9: 1 =9
18 : 2 = 9
27 : 3 = 9
54 : 6 = 9
90 : 10 = 9
182 : 18 = 9

Bei Aufgaben in Mathematik zur direkten Proportionalität ist es an der Realschule Bayern sehr häufig so, dass Lücken in Wertetabellen gefüllt oder Zahlenpaare auf direkte Proportionalität geprüft bzw ergänzt werden sollen.

Ursprungshalbgerade als Graph bei einer direkten Proportionalität

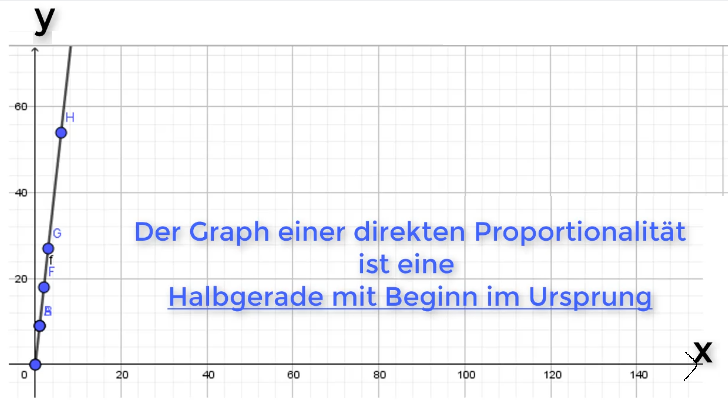
Die Zahlenpaare (xIy) stellen Punkte im Koordinatensystem dar. Überträgst du diese nun in ein Koordinatensystem und verbindest sie zu einem Graph, so entsteht eine Ursprungshalbgerade. Immer wenn eine direkte Proportionalität vorliegt, muss eine Ursprungshalbgerade entstehen. Umgekehrt gilt auch: Liegt eine Ursprungshalbgerade als Graph vor, so handelt es sich um eine direkte Proportionalität.

Eine Halbgerade ist unendlich lange (kein Ende) und hat immer einen Beginn. Dieser ist bei der direkten Proportionalität immer im Punkt (0I0), dem Ursprung.

Direkte Proportionalität und Beispiele für die Anwendung

Das Thema „Direkte Proportionalität“ ist im Lehrplan Mathematik der Realschule Bayern in der 6. Klasse verankert. Im gleichen Themenblock wird die Prozentrechnung gelernt, da hier ein Zusammenhang besteht. Rechnet man beispielsweise von 100 % auf 1 % und dann auf 15 % „hoch“, so funktioniert das, weil auch hier eine direkt proportionale Zuordnung vorliegt. Der Dreisatz basiert ebenso auf der direkten Proportionalität.
In der 7. Klasse Mathematik der Realschule Bayern lernst du eine weitere Zuordnung: Die indirekte Proportionalität.
In 8I bzw. 9II/III wird das Thema „Direkte Proportionalität“ erneut aufgegriffen und hin zur „Linearen Funktion“ erweitert.

Im Alltag findest du zahlreiche Beispiele für eine direkt proportionale Zuordnung:
100 g Wurst kosten x, was kosten 400 g?
1 Kugel Eis kostet x, was kosten 7 Kugeln?
usw.

Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du anschauliche Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter zum Ausdrucken.