Aufgaben zur Exponentialfunktion:
Wachstumsprozesse bzw. Zerfallsprozesse

In der 10. Klasse (Mathe Realschule) lernst du eine neue Funktion kennen, die sogenannte Exponentialfunktion.
Diese Exponentialfunktion zeichnet sich durch ihre einzigartige Eigenschaft aus, dass die Variable x im Exponent auftaucht. Dadurch erhält sie ihren besonderen Namen und eröffnet uns neue Dimensionen mathematischer Zusammenhänge.
Du kennst bereits vom Thema Potenzen, dass hier die Basis stets mit sich selbst multipliziert wird. Durch diese Multiplikation nimmt das Ergebnis zunächst langsam zu und dann nach und nach immer schneller und schneller. Somit ergibt sich bei Wachstumsprozessen der im Bild gezeigte Verlauf des Graphen.
Auch Zerfallsprozesse können mithilfe einer Exponentialfunktion beschrieben werden. In der Mathe-Abschlussprüfung tauchen so zum Beispiel Aufgaben auf, in denen Milchschaum zerfällt, Getränke abkühlen, Autos an Wert verlieren usw.
Schauen wir uns nun ein Beispiel zu einem Wachstumsproezss der Exponentialfunktion an.

Beispiel-Aufgabe Exponentialfunktion (Wachstumsprozess):

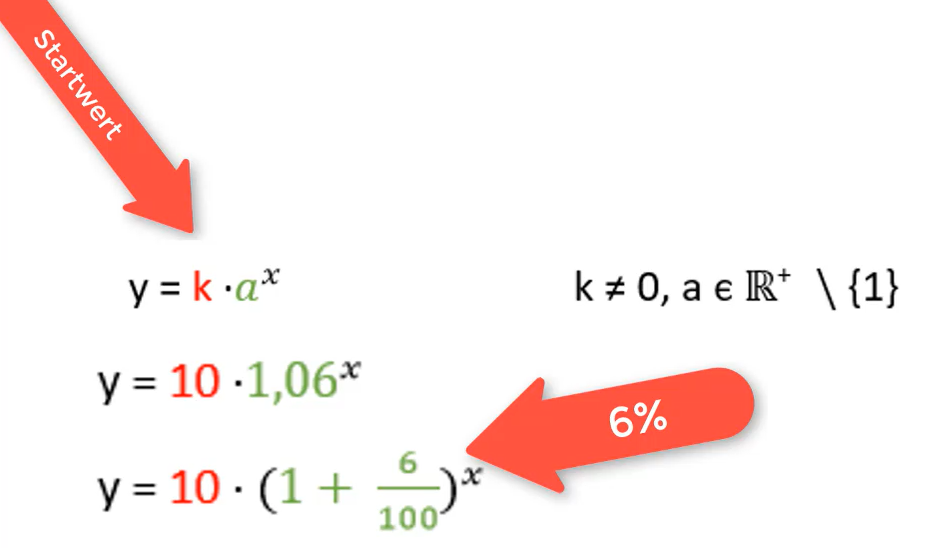
Bei jeder Exponentialfunktion beschreibt der Faktor k den Start- oder Anfangswert. In diesem Beispiel stellt dies den Wert einer Aktie dar.
Die Basiszahl (hier: 1,06) legt das Wachstum fest und bestimmt den Verlauf des Graphen.
In der 10. Klasse (Mathe Realschule) bearbeitest du hierzu Aufgaben.

Willkommen auf dieser Mathe-Lernplattform: Hier erwarten dich verständliche Mathe-Lernvideos, passende Übungen und unterstützende Arbeitsblätter zum Ausdrucken.

Graph der Exponentialfunktion (zu Aktien-Beispiel):

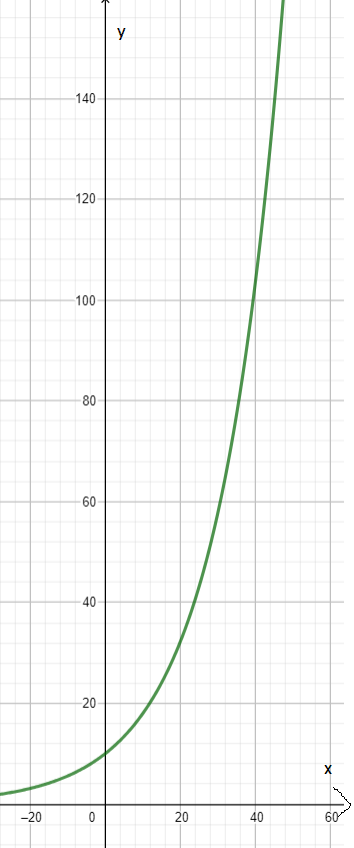
In diesem Beispiel verläuft der Graph der Exponentialfunktion durch den Punkt (oI10), da k den Wert 10 hat. Der Graph steigt nicht gleichmäßig oder linear an, sondern zuerst langsam und dann immer schneller. Ein deutliches exponentielles Wachstum ist zu erkennen.

Allgemein gilt:
– Wenn k>0 und a>1 sind, beschreibt die Exponentialfunktion einen Wachstumsprozess.
– Wenn k>0 und a<1 sind, beschreibt die Exponentialfunktion einen Zerfallsprozess/Abklingprozess. Der Graph fällt erst schnell und dann immer langsamer ab.
– Bei k<0 liegen die Graphen der Exponentialfunktion unterhalb der x-Achse.

Bei der linearen Funktion hingegen war der steigende oder fallende Verlauf gleichmäßig durch die Steigung m festgelegt. Alle lineare Funktionen haben die Form y = mx + t.
Bei der quadratischen Funktion (Parabel) taucht die Variable x immer mit dem Exponent 2 auf, sodass alle quadratischen Funktionen die Form y=ax²+bx+c besitzen.

Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Übungen, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter mit Matheaufgaben, die du sogar ausdrucken kannst. Übe Mathe online mit einer Realschullehrerin.

Exponentialfunktion in der Abschlussprüfung (Mathe Realschule):
Beispiele Wachstumsprozesse

Ab dem Schuljahr 2023/2024 kann das Thema Exponentialfunktion wieder in der Mathe-Abschlussprüfung (Realschule Bayern) abgefragt werden. Zwei Aufgabentypen sind möglich – Wachstumsprozesse bei Exponentialfunktionen oder auch Zerfallsprozesse.
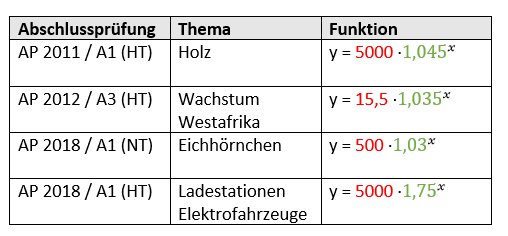
Eine Exponentialfunktion beschreibt einen Wachstumsprozess, wenn die Basis der Potenz (grün markiert) einen Wert >1 aufweist.
Hier siehst du eine Übersicht mit Beispielen zu Exponentialfunktionen mit Wachstumsprozessen:

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen, um online Mathe zu üben. Außerdem gibt’s hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Exponentialfunktion in der Abschlussprüfung (Mathe Realschule):
Beispiele Zerfallsprozesse

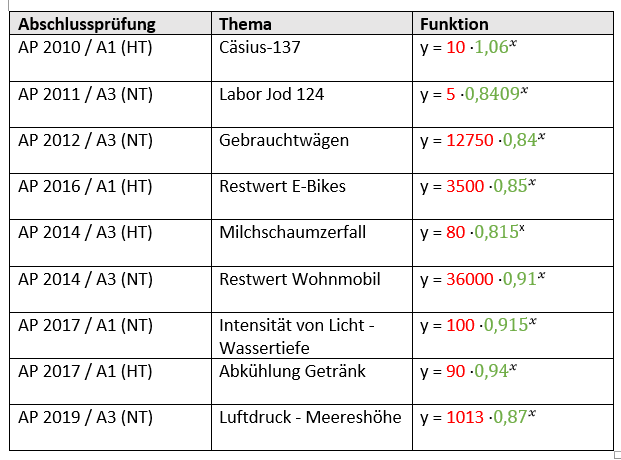
Eine Exponentialfunktion beschreibt einen Zerfallsprozess / Abklingprozess, wenn die Basis der Potenz (grün markiert) < 1 ist.
Der Graph dieser Exponentialfunktion ist durch einen fallenden Verlauf gekennzeichnet. Der Abfall ist zunächst sehr stark und flacht dann ab. Hier siehst du in welchen Jahren (Mathe Abschlussprüfung Realschule Bayern) beispielsweise die Exponentialfunktion in Zusammenhang mit einem Zerfallsprozess abgefragt wurde:

Entdecke eine innovative Mathe-Lernplattform: Hier erwarten dich interaktive Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter zum Ausdrucken.

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.