Kongruente Dreiecke – Kongruenzabbildungen (Achsenspiegelung, Parallelverschiebung, Drehung)

Dreiecke sind kongruent, also deckungsgleich, wenn diese exakt die gleiche Größe bzw. Form haben. Du kannst dir vorstellen, dass die Dreiecke exakt aufeinander passen müssen, wenn du Ur- und Bilddreieck ausschneidest.
Natürlich wäre es umständlich, wenn du jedes Mal eine Vorlage basteln musst und durch Ausschneiden die Kongruenz von Dreiecken überprüfen müsstest.

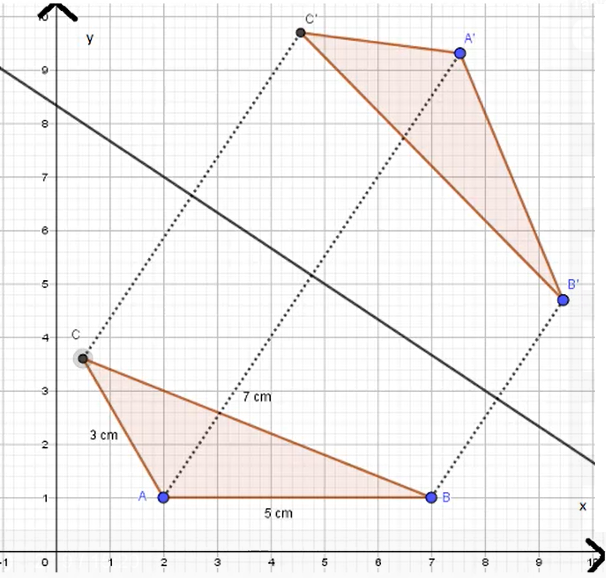
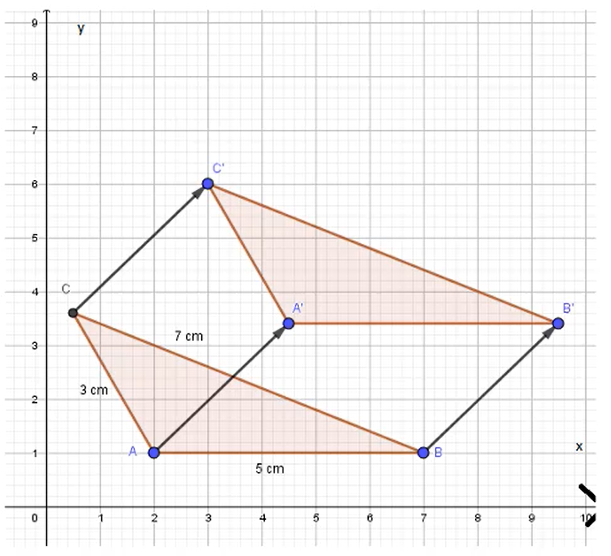
Wenn Figuren durch eine Kongruenzabbildung (z.B. Achsenspiegelung, Parallelverschiebung oder Drehung) abgebildet wurden, kannst du sicher sein, dass Ur- und die neu entstandene Bildfigur kongruent sind.

Natürlich ist es auch möglich, dass mehrere Kongruenzabbildungen nacheinander ausgeführt werden. Beispielsweise wird eine Urfigur zunächst an einer Spiegelachse gespiegelt und anschließend um ein Drehzentrum gedreht. Die neue Bildfigur ist nach wie vor kongruent zur Urfigur, auch wenn mehrere Kongruenzabbildungen durchgeführt wurden. Bei einer Hintereinanderausführung kann es sein, dass es schwerer wird nachzuvollziehen, ob die Dreiecke kongruent sind.

Abhilfe schaffen hierfür die gültigen Kongruenzsätze:

– sss-Satz

– sws-Satz

– ssw-Satz

-sSwg-Satz
Die Kongruenzsätze ermöglichen es ganz leicht kongruente Dreiecke zu erkennen und dies auch mathematisch zu begründen, dass diese kongruent zueinander sein müssen.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe online Mathe mit einer Realschullehrerin.

Kongruenzsatz: sss-Satz

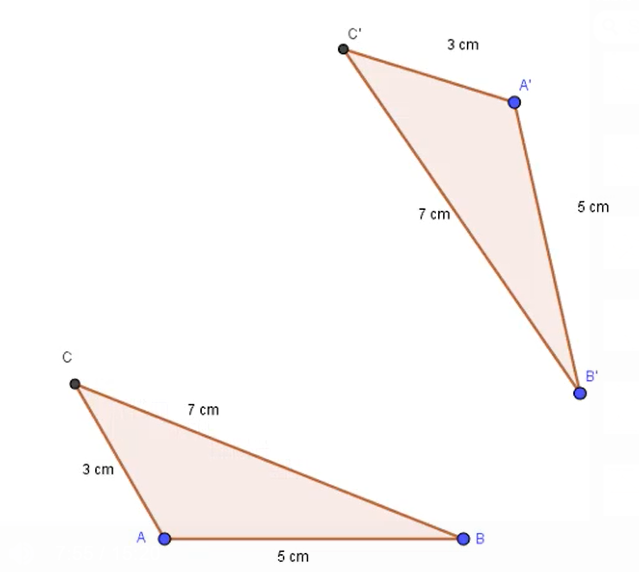
Der Kongruenzsatz sss greift, wenn bei Dreiecken drei Seitenlängen gegeben sind und diese übereinstimmen. Hier in diesem Beispiel gilt a = 7 cm, b = 3 cm und c = 5 cm. Das zweite Dreieck hat a`=7cm, b`=3 cm und c`= 5 cm. Nachdem beide Dreiecke in den Seitenlängen übereinstimmen, kann nach dem sss-Satz ganz sicher gesagt werden, dass diese Dreiecke kongruent zueinander sind. Es müssen nicht a und a`, b und b`, c und c`übereinstimmen, entscheidend ist nur, dass jede Seitenlänge auch im anderen Dreiecken mit exakt der gleichen Länge auftaucht.

Nachdem der sss-Kongruenzsatz greift, weißt du auch ganz sicher, dass du diese Dreiecke konstruieren kannst. Der Kongruenzsatz besagt, dass dieses Dreieck existiert und eindeutig festgelegt ist.

Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du anschauliche Mathe-Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Lerne und übe Mathe online mit einer Realschullehrerin.

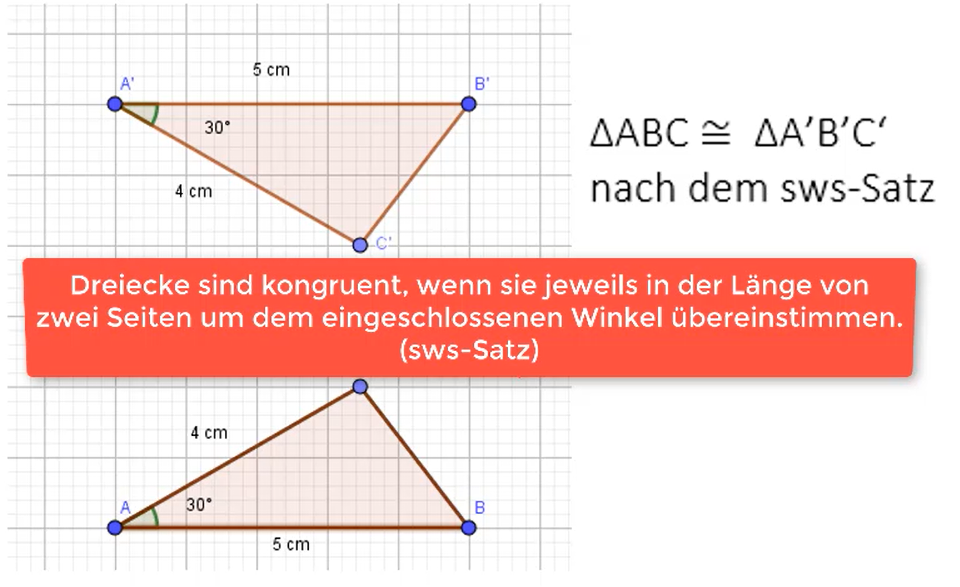
Kongruenzsatz: sws-Satz

Der Kongruenzsatz sws greift, wenn bei Dreiecken zwei Seiten und der eingeschlossene Winkel gegeben sind, daher der Name sws. Die Reihenfolge der Buchstaben dient als kleine Merkhilfe, dass der Winkel zwischen den beiden bekannten Seiten liegen muss. In diesem Beispiel siehst du, dass die Dreiecke kongruent sind, da beide Dreiecke Seitenlängen von 4 cm und 5 cm haben und der eingeschlossene Winkel in beiden Dreiecken 30° beträgt.
Aufgrund dieser Übereinstimmung, kannst du direkt sagen, dass die Dreiecke nach dem sws-Satz kongruent sind.
Die Schreibweise hierfür siehst du auf der Grafik.

Dadurch, dass der sws-Kongruenzsatz greift, kannst du das auch sicher sagen, dass diese Dreiecke existieren (du kannst sie zeichnen) und es gibt nur eine Möglichkeit wie du sie zeichnen kannst.

Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von interaktiven Erklärvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu meistern.

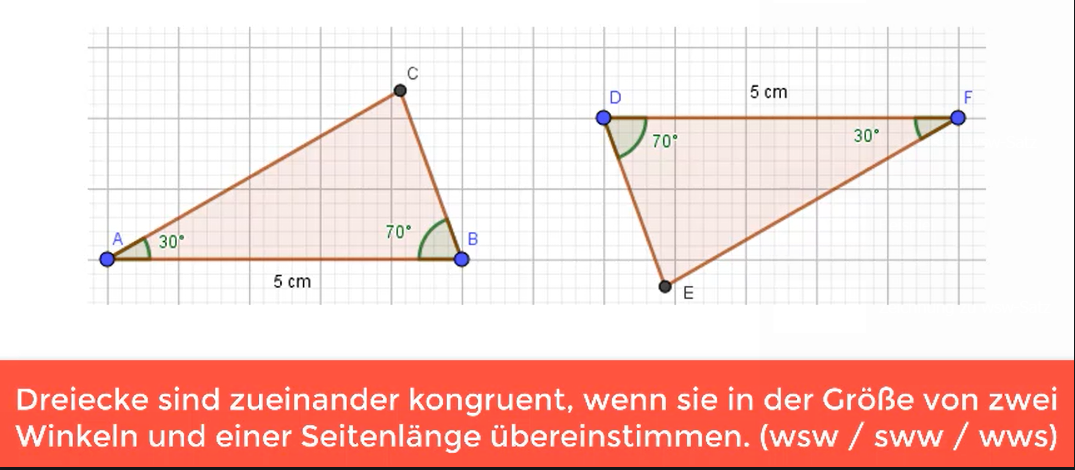
Kongruenzsatz: sww-Satz, wws-Satz, wsw-Satz

Dreiecke sind kongruent, wenn sie den sww-Satz erfüllen. Der sww-Satz ist identisch mit dem wws-Satz oder auch dem sww-Satz. Du siehst, dass bei allen drei Formulierungen 2 x w und 1 x s auftauchen. Das bedeutet, dass dieser Kongruenzsatz genau dann greift, wenn in Dreiecken zwei Winkel und eine Seite gegeben sind und diese mit den Maßen im anderen Dreieck übereinstimmen. Im Gegensatz zum sws-Kongruenzsatz muss hier der Winkel nicht zwischen den beiden gegebenen Seiten liegen, sondern kann an beliebiger Stelle im Dreieck liegen.
Du siehst, dass in diesem Beispiel die gegebene Seite mit 5 cm in beiden Dreiecken auftaucht. Beide Dreiecke haben Winkel von 30° und 70°. Aufgrund der Innenwinkelsumme im Dreieck, muss auch der dritte Winkel im Dreieck übereinstimmen.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Lernvideos, passende Übungen und nützliche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe Mathe online.

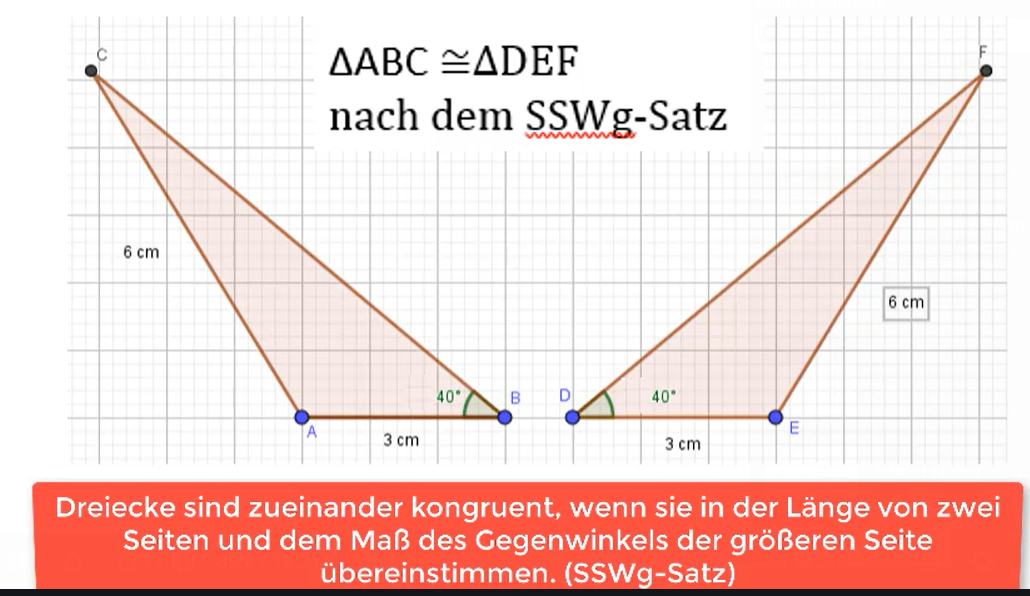
Kongruenzsatz – sSwg-Satz

Der Kongruenzsatz sSwg-Satz greift, wenn bei Dreiecken die Länge von zwei Seiten und ein Winkelmaß gegeben ist. Der Kongruenzsatz heißt sSwg, da es nicht reicht, wenn ein beliebiger Winkel im Dreieck gegeben ist. Es muss der Winkel gegeben sein, der der längeren der beiden Seiten gegebenüber liegt. Nur wenn beide Seiten und dieser Winkel in beiden Dreiecken übereinstimmen, sind diese nach dem sSwg-Satz kongruent.
Im oberen Beispiel siehst du, dass hier der sSwg-Satz greift, da beide Seitenlängen mit 6 cm und 3 cm haben. Der gegebene Winkel von 40° liegt gegenüber von der längeren Seite. Die Dreiecke sind nun nach dem sSwg-Satz kongruent.

Entdecke die faszinierende Welt der Mathematik online: Hier erwarten dich inspirierende Lernvideos, herausfordernde interaktive Übungen und praktische Arbeitsblätter mit Matheaufgaben, die du einfach ausdrucken kannst.

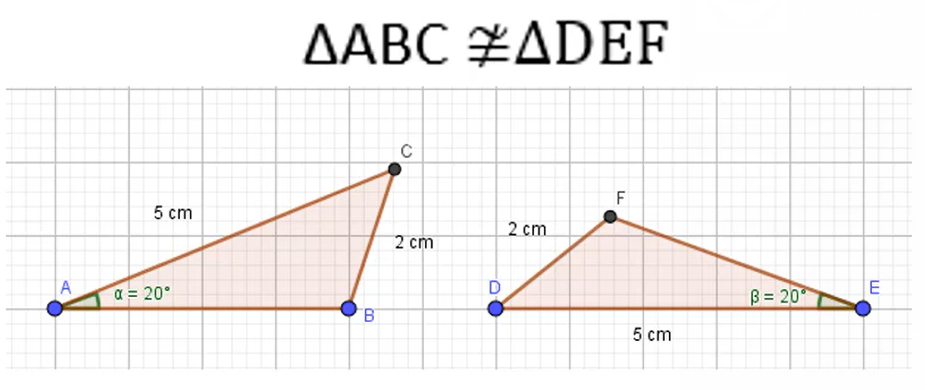
 In diesem Beispiel greift der sSwg-Kongruenzsatz nicht. Es sind hier zwei Seiten gegeben, mit 5 cm und 2 cm. Der gegebene Winkel von 20° muss nun gegenüber der längeren der beiden Seiten liegen, damit der sSwg-Satz gilt. Nachdem in diesem Beispiel jedoch die 20° gegenüber der kürzeren der beiden Seiten liegt, sind hier die Dreiecke nicht kongruent. Der Kongruenzsatz sSwg-Satz greift hier nicht. Es könnte sein, dass diese Dreiecke kongruent sind, das muss aber nicht so sein. Es kann in diesem Fall keine eindeutige Aussage getroffen werden.

Zusammenfassend lässt sich sagen: Greift einer der Kongruenzsätze (sss-Satz, sws-Satz, sww-Satz oder der sSwg-Satz), so kannst du mathematisch begründen, dass die entsprechenden Dreiecke kongruent sind.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.