Lineare Funktion – Lernvideos und Aufgaben (Mathe 9. Klasse)
Lineare Funktion: Funktionsterm, Funktionsgleichung und Funktionswerte
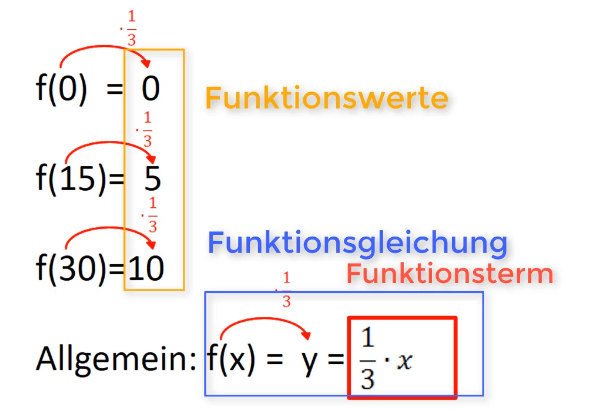
Bei Funktionen müssen die Begriffe „Funktionsterm„, „Funktionsgleichung“ und „Funktionswerte“ unterschieden werden. Beginnen wir mit dem „Funktionsterm„: 1/3x ist hier der Funktionsterm. Dieser ist immer nach dem Schema m*x bei linearen Funktionen aufgebaut. Der Faktor (m) vor dem x gibt immer die Steigung der linearen Funktion an. Der Graph einer linearen Funktion ist immer eine Gerade. Ist m positiv, so steigt die Gerade, ist m negativ, so fällt diese.
Als Funktionsgleichung wird der Aufbau mit y = m*x bzw. y = m*x + t bezeichnet.
Für die Variable x können nun Werte aus der Grundmenge eingesetzt werden. Die y-Werte, die sich dann ergeben, werden als Funktionswerte bezeichnet. Die x-und y-Werte werden anschließend übersichtlich in Form einer Wertetabelle dargestellt werden. Überträgst du nun zwei oder mehr Punkte in ein Koordinatensystem und verbindest diese, so entsteht der Graph, eine Gerade.
Graph einer linearen Funktion zeichnen mithilfe einer Wertetabelle
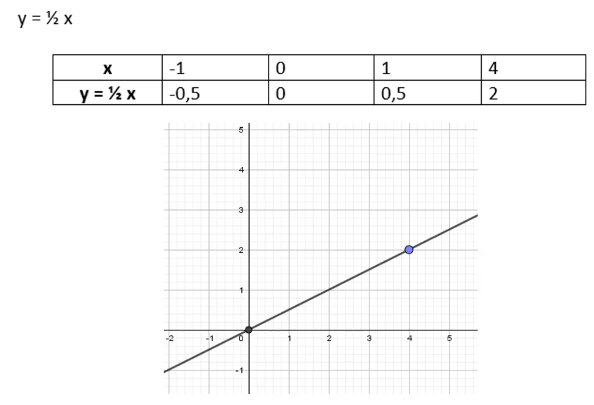
Weiteres Beispiel: y = 1/2x
1/2x ist ein Funktionsterm. y = 1/2x ist eine Funktionsgleichung.
Erstelle für die Funktion y = 1/2x eine Wertetabelle, indem du für die Variable x nacheinander Werte einsetzt (hier: -1; 0; 1; 4). Die Funktionswerte (y-Werte) ergeben sich somit folgendermaßen:
f(-1) = 1/2 * (-1) = -1/2
f(0) = 1/2 * 0 = 0
f(1) = 1/2 * 1 = 1/2
f(4) = 1/2 * 4 = 2
Trägst du nun mindestens zwei von den Punkten (-1/-0,5); (0/0); (1/0,5); (4/2) in ein Koordinatensystem ein und verbindest diese zu einem Graph, so ensteht bei linearen Funktionen immer eine Gerade. Eine Gerade wird immer durch zwei Punkte eindeutig festgelegt, deshalb mindestens zwei.
Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Übungen, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter mit Matheaufgaben, die du sogar ausdrucken kannst. Übe Mathe online mit einer Realschullehrerin.
Hier geht’s zu Mathe-Videos & Aufgaben
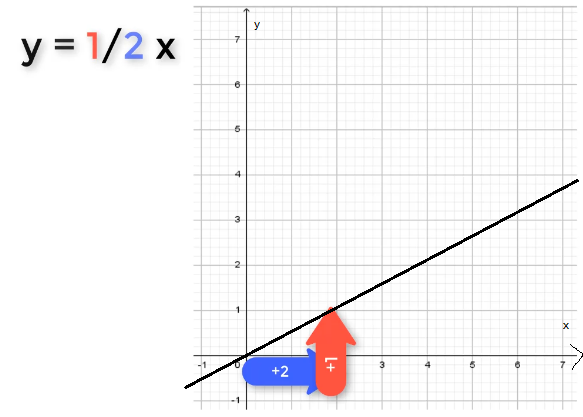
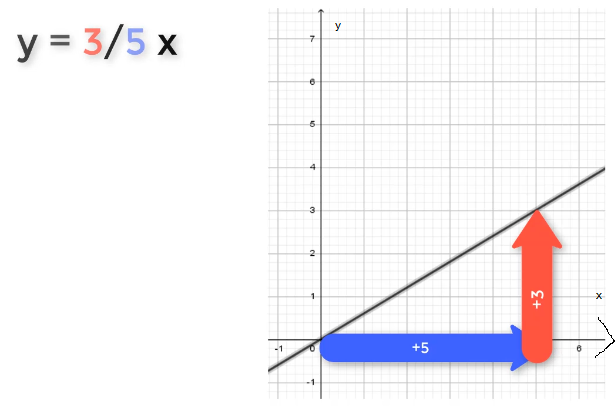
Graph einer linearen Funktion zeichnen mithilfe eines Steigungsdreiecks
Eine lineare Funktion hat immer die Form y = m * x. Der Faktor m gibt stets die Steigung der Gerade an. Der Nenner (hier: 2) gibt an, wie viele Einheiten du in x-Richtung antragen musst. Der Zähler (hier: 1) zeigt die y-Richtung des Steigungsdreiecks an.
Die rechnerische Erklärung hierfür ergibt sich aus der Umformung folgender Geradengleichung:
y = m * x / : x
y/x = m
Somit steht im Nenner immer die x-Richtung und im Zähler die y-Richtung des Steigungsdreiecks.
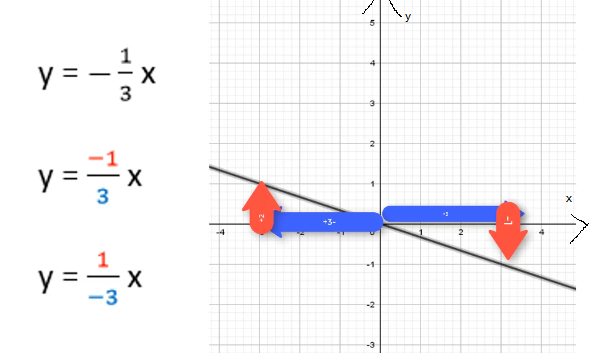
Steigungsdreieck: m < 0 y = m*x
Liegt eine lineare Funktion mit negativem m vor, so weißt du, dass diese Gerade fällt. Der Verlauf des Graphen ist also von links oben nach rechts unten. Das „-“ kann entweder komplett vor dem Bruch stehen, in den Zähler oder in den Nenner „gezogen“ werden. Alle drei Schreibweisen sind richtig und stellen dieselbe lineare Funktion dar.
Für das Steigungsdreieck bedeutet das, dass du entweder 3 Einheiten (meist Zentimeter oder Kästchen) nach rechts und eine Einheit nach unten musst. Zweite Möglichkeit: Du trägst 3 Einheiten nach links an, da -3 im Nenner steht und dafür 1 nach oben. Verbindest du nun zu einem Graph, so erkennst du, dass für beide Steigungsdreiecke dieselbe Gerade entsteht.
Auf dieser Lernplattform entdeckst du die Welt der Mathematik online: Hier findest du inspirierende Mathe-Lernvideos, herausfordernde interaktive Übungen und nützliche Arbeitsblätter mit Matheaufgaben, die du bequem ausdrucken kannst. Übe online Mathe mit einer Mathelehrerin.
Hier geht’s zu Mathe-Videos & Aufgaben
Lineare Funktion: y = m*x+t mit t als y-Achsensabschnitt
Jede lineare Funktion hat folgenden Aufbau: y = m*x + t. Während m die Steigung der Gerade angibt (m > 0: steigende Gerade; m > 0: fallende Gerade), beschreibt t den y-Achsenabschnitt. Der y-Achsenabschnitt t gibt den Schnittpunkt der Gerade mit der y-Achse an. Das bedeutet: Wo durchkreuzt die Gerade die y-Achse?
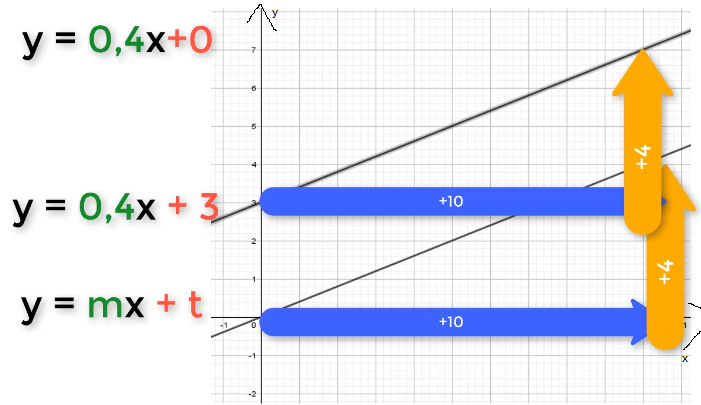
Bisher haben wir lineare Funktionen mit dem Aufbau y = m*x +0 betrachtet. Hier war t = 0, deshalb handelt es sich um Ursprungsgeraden.
Im oberen Beispiel gilt für m = 0,4 = 4/10. Nachdem für t = 3 gilt, wird nun auf dieser y-Höhe das Steigungsdreieck angetragen (10 nach rechts; 4 nach oben)
Immer wenn m als Dezimalzahl angegeben ist, kannst du diese jederzeit in einen Bruch umwandeln, um so leichter das Steigungsdreieck zu erkennen. Wenn du nicht mehr sicher bist wie du Dezimalzahlen in Brüche umwandelst, klicke hier.
Lineare Funktion: y = m*x+t im Lehrplan der Realschule Bayern
In der 6. Klasse Mathematik lernen die Schüler*innen die „Direkte Proportionalität“. Bei jeder direkten Proportionalität entsteht eine Ursprungshalbgerade als Graph. Alle Geraden bilden lineare Funktionen, die in der 8. Klasse Realschule dann behandelt werden. Ein kleiner Ausblick: In der 10. Klasse Mathematik (10II/III) bzw. 9 I Mathematik werden dann noch Quadratische Funktionen betrachtet und in der Abschlussprüfung geprüft.
Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen, um online Mathe zu üben. Außerdem gibt’s hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.
Hier geht’s zu Mathe-Videos & Aufgaben