Mittelsenkrechte (Zeichnung und Konstruktion) – Lernvideos und Aufgaben (Mathe 6. Klasse)
Was ist eine Mittelsenkrechte?
Eine Mittelsenkrechte ist eine Gerade. Diese steht senkrecht zu einer beliebigen Strecke, deshalb taucht das Wort „senkrecht“ im Wort „Mittelsenkrechte“ auf. Diese Senkrechte verläuft exakt durch den Mittelpunkt der Strecke, daher die Bezeichnung „Mittelsenkrechte“.
Wie du eine Mittelsenkrechte mit Geodreieck zeichnest und auch mit Zirkel und Lineal konstruierst, lernst du in Mathematik in der 6. Klasse (Realschule Bayern).
Im Lehrplan der Realschule Bayern taucht diese im Themenbereich der „Achsenspiegelung“ auf, da es sich bei der Spiegelachse auch um eine Mittelsenkrechte handelt.
Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Lernvideos, spannende Übungen und praktische Arbeitsblätter zum Drucken.
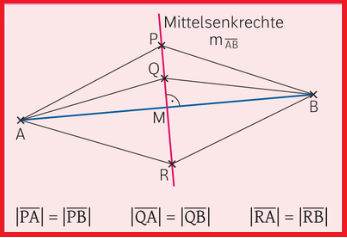
Welche Eigenschaften hat eine Mittelsenkrechte?
Alle Punkte, die auf der Mittelsenkrechte liegen, haben eine gemeinsame Eigenschaft: Sie liegen alle gleich weit von A bzw. B, entfernt. Die mathematische Kurzschreibweise hierfür siehst du auf dem Bild. Die Strecke vom Mittelpunkt zu A bzw. vom Mittelpunkt zu B ist hierbei am Kürzesten.
Wie zeichnest du eine Mittelsenkrechte?
Gehe so vor:
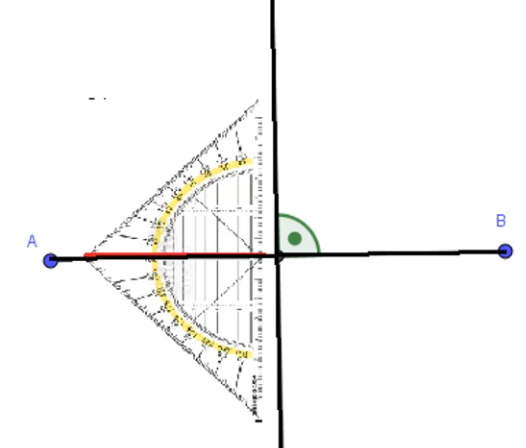
Möchtest du eine Mittelsenkrechte zeichnen, so benötigt du am Besten ein Geodreieck und einen Bleistift.
Schritt 1: Miss die Länge der Strecke.
Schritt 2: Markiere den Mittelpunkt der Strecke.
Schritt 3: Lege das Geodreieck mit der Nulllinie auf die Strecke, damit du eine Senkrechte durch den Mittelpunkt antragen kannst. (siehe Zeichnung oben)
FERTIG!
Mittelsenkrechte konstruieren (mit Zirkel und Lineal): Schritt für Schritt
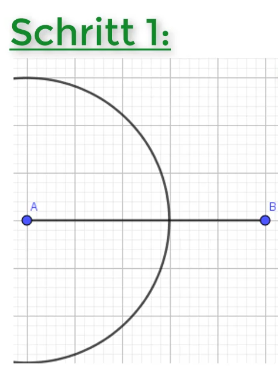
Du sollst zu einer gegebenen Strecke die Mittelsenkrechte konstruieren. Im ersten Schritt stichst du in einen Streckendpunkt mit dem Zirkel ein. Wähle einen beliebigen Kreisradius. Beachte nur, dass der Radius groß genug ist! Groß genug heißt, dass der Radius größer als die Hälfte der Strecke sein muss, da sich sonst die beiden Halbkreise nicht schneiden.
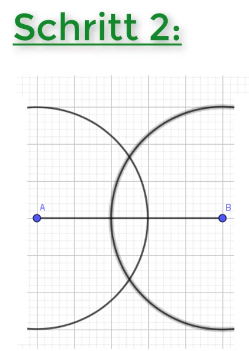
Im zweiten Schritt stichst du mit dem gleichen Radius in den anderen Punkt ein, hier B. Zeichne nun einen weiteren Halbkreis. Die beiden Halbkreise müssen sichtbar sein, da es sich um die Konstruktion der Mittelsenkrechte handelt.
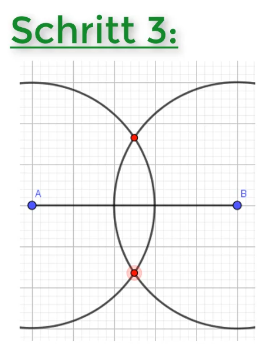
Im dritten Schritt der Konstruktion der Mittelsenkrechte markierst du die beiden Schnittpunkt der Halbkreise.
Jetzt klärt es sich auch, warum der gewählte Radius der Halbkreise über die Mitte hinausragen mussten. Ist der Radius zu klein, gibt es keinen Schnittpunkt.
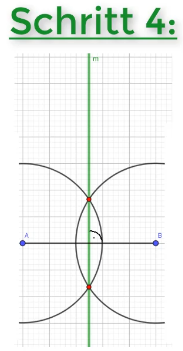
Schritt 4 der Konstruktion der Mittelsenkrechte ist nun, dass du die beiden Schnittpunkte zu einer Gerade verbindest. Diese Gerade ist nun die Mittelsenkrechte.
Wichtig: Bei der Konstruktion müssen Zirkelspuren erkennbar sein!