Parallelverschiebung – Lernvideos und Aufgaben (Mathe 7. Klasse)
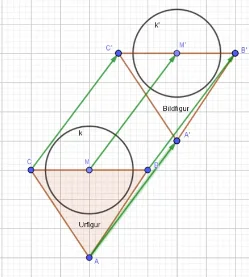
Die Parallelverschiebung ist eine Abbildung, bei der jedem Urpunkt P (Punkt der ursprünglichen Figur) jeweils ein Bildpunkt P‘ (Punkt der Figur nach der Abbildung) zugeordnet wird. Die Zuordnung erfolgt durch einen Pfeil / Vektor.
Hier geht’s zu Mathe-Videos & Aufgaben
Was sind Vektoren?
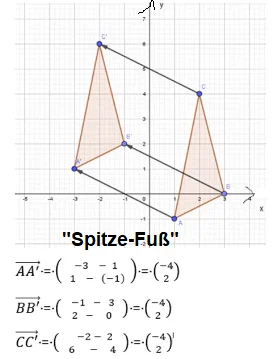
Trage von jedem Urpunkt P aus den Verschiebungspfeil (=Vektor) an und du erhältst den zugehörigen Bildpunkt P‘. Der Verschiebungspfeil PP‘ beispielsweise beginnt im Punkt P und zeigt mit der Pfeilspitze zu P‘. Der Startpunkt heißt „Fuß“, der andere „Spitze“. Der Vektor P’P hingegen hat seinen Fuß im Punkt P‘ und seine Spitze bei P.
Die Verschiebungspfeile (=Vektoren) haben stets folgende Merkmale:
- Parallel
- Gleich lang
- Gleich gerichtet, d.h. dass diese in die gleiche Richtung zeigen.
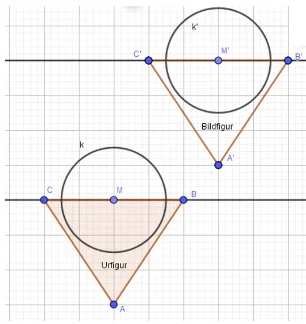
Parallelverschiebung als Kongruenzabbildung:
Ur- und Bildfigur, die lediglich durch einen Vektor verschoben wurden, sind stets kongruent (=deckungsgleich). Somit liegt bei der Parallelverschiebung eine Kongruenzabbildung vor.
In der 6. Klasse Mathe der Realschule Bayern hast du bereits die Achsenspiegelung als Kongruenzabbildung gelernt, im Lehrplan der Realschule folgt in der 7. Klasse nun die Parallelverschiebung.
Die Urfigur ist stets gegen den Uhrzeigersinn (UZS) beschriftet, das bleibt auch durch die Parallelverschiebung unverändert. So gilt, dass Ur- und Bildfigur den gleichen Umlaufsinn, also die gleiche Reihenfolge der Beschriftung, haben.
Wie viele Fixpunkte hat eine Parallelverschiebung?
Bei einer Parallelverschiebung werden alle Urpunkte durch einen Verschiebungspfeil / Vektor verschoben, sodass kein einziger Punkt an der gleichen Stelle bleibt. Aufgrund dieser Tatsache gibt es bei der Parallelverschiebung keinen Fixpunkt.
Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von interaktiven Mathe-Lernvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu üben.
Hier geht’s zu Mathe-Videos & Aufgaben