Binomische Formeln – Lernvideos und Aufgaben (Mathe 8. Klasse)
Binomische Formeln – Was ist das und was ist der Vorteil?
Ein „Binom“ ist eine Summe mit zwei Summanden, z.B. x + 1. Das Quadrat eines Binoms (Exponent 2) kannst du immer wie in diesem Beispiel berechnen:
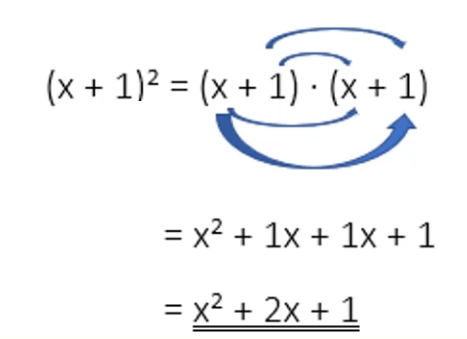
In diesem Beispiel wurden die Summenterme x+1 und x+1 multipliziert und somit die Klammer aufgelöst. Nachdem die beiden Summterme jeweils mit sich selbst multipliziert wurden, gibt es einen schnelleren/einfacheren Weg.
Die Binomischen Formeln ermöglichen es, dass du nicht mehr ausmultiplizieren musst, sondern durch Einsetzen in die Formel das Ergebnis des vereinfachten Terms erhältst.
Auf dieser Lernplattform kannst du Mathe online lernen: Du findest Mathe-Lernvideos, interaktive Übungen und Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe hier online Mathe mit einer Realschullehrerin.
Hier geht’s zu Mathe-Videos & Aufgaben
Erste Binomische Formel – Beispiele
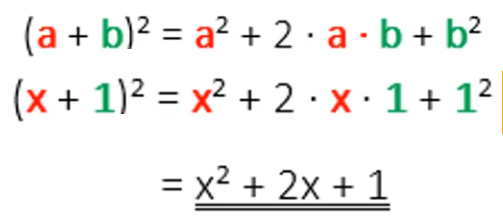
Multiplizierst du die beiden Summenterme (a+b) * (a+b), dann erhältst du als Ergebnis a² + 2ab + b².
Im linken Beispiel gilt: a = x und b = 1. Nun kannst du in die Formel anstelle von a und b einsetzen und ersparst dir das Ausmultiplizieren der Summenterme.
Im rechten Beispiel gilt: a = 2x und b = 4. Wenn du anstelle von a die 2x einsetzt, musst du Klammern setzen, damit nicht nur das x quadriert wird, sondern das „gesamte Paket“. (2x)² = 2x * 2x = 4x².
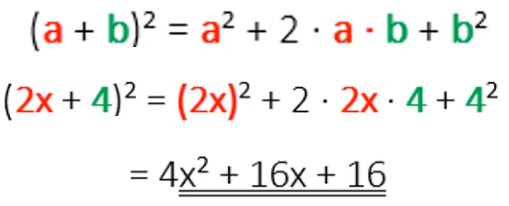
Zweite Binomische Formel – Beispiele
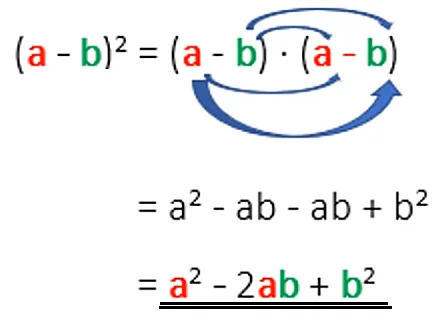
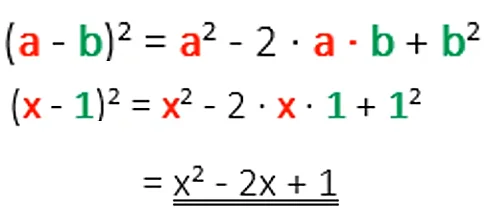
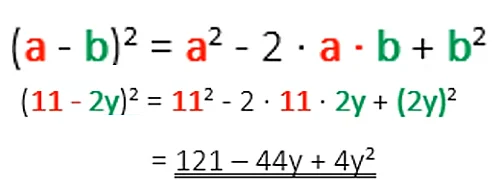
Multiplizierst du die beiden Summenterme (a-b) * (a-b), dann erhältst du als Ergebnis a² – 2ab + b².
Im linken Beispiel gilt: a = x und b = 1. Nun kannst du in die Formel anstelle von a und b einsetzen und ersparst dir das Ausmultiplizieren der Summenterme.
Im rechten Beispiel gilt: a = 11 und b = 2y. Wenn du anstelle von b die 2y einsetzt, musst du wie im oberen Beispiel Klammern setzen.
Dritte Binomische Formel – Beispiele
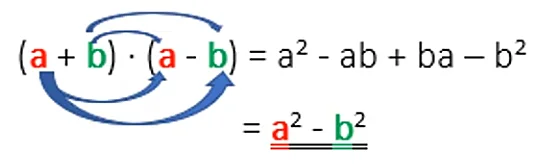
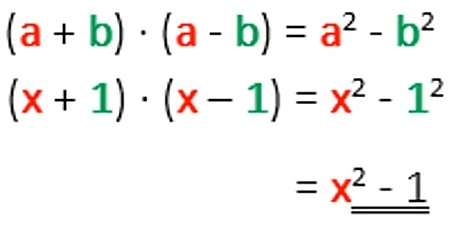
Die 3. Binomische Formel lautet: (a+b)*(a-b) = a² – b². a bzw. b müssen bei beiden Summentermen identisch sein, lediglich die Vorzeichen unterscheiden sich.
Bei der Aufgabe (a-b)*(a+b) handelt es sich ebenso um die 3. Binomische Formel, da hier aufgrund des Kommutativgesetzes jederzeit die Reihenfolge verändert werden kann, ohne dass sich am Ergebnis etwas ändert.
Hast du eine Aufgabe vorliegen mit verschiedenen Summentermen, so musst du ausmultiplizieren und kannst keine Binomische Formel anwenden:
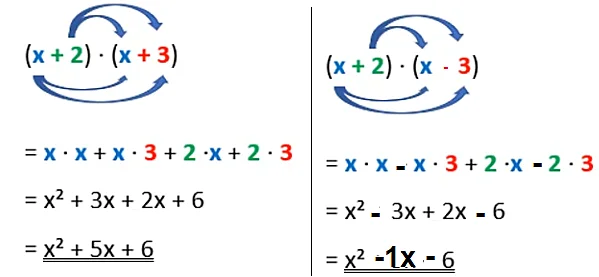
Binomische Formeln im Lehrplan PLUS der Realschule Bayern
In der 8. Klasse Mathematik der Realschule Bayern taucht ein großer Themenblock auf, der sich damit befasst Terme zu vereinfachen. Mithilfe von Binomischen Formeln ist es oft möglich Terme zu vereinfachen. Wie das funktioniert, erfährst du hier anhand von Beispielen.
Quadratische Terme (mit ²) spielen auch eine besondere Rolle in der 8. Klasse. Mithilfe der Binomischen Formeln ist es möglich den Extremwert von quadratischen Termen (Minimum/Maximum) zu ermitteln.
In der 8. Klasse tauchen auch „Lineare Gleichungen / Ungleichungen“ erneut auf, in denen ab dann auch Binomische Formeln autreten können.
Entdecke auf dieser Lernplattform die faszinierende Welt der Mathematik: Verbessere spielerisch deine Fähigkeiten mit interaktiven Übungen, tauche ein in informative Mathe-Lernvideos und nutze hochwertige Arbeitsblätter mit Matheaufgaben, die du sogar ausdrucken kannst. Übe gleich online.
Hier geht’s zu Mathe-Videos & Aufgaben
