Zentrische Streckung – Lernvideos und Aufgaben (Mathe 9. Klasse)
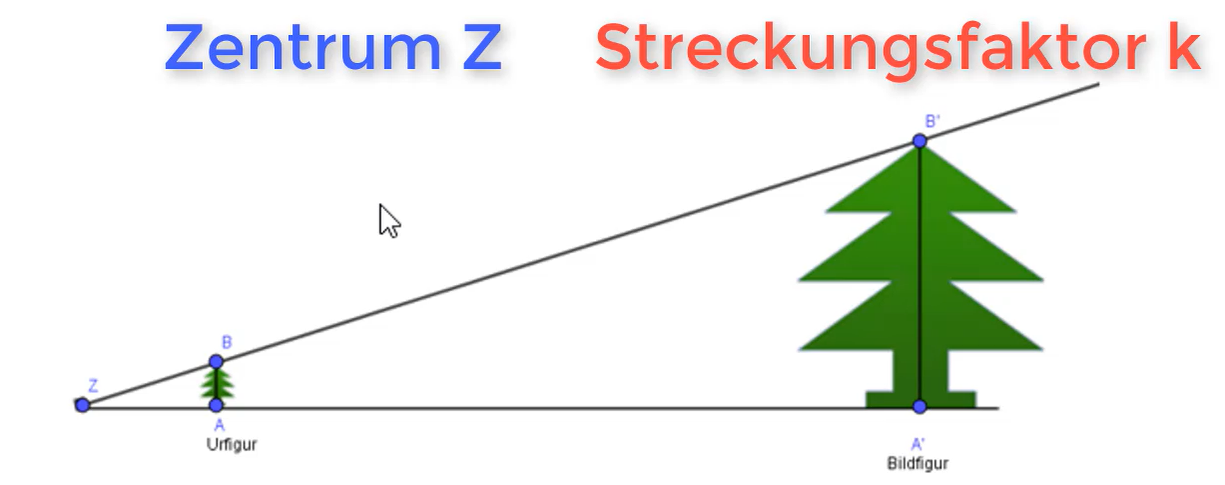
Abbildung durch zentrische Streckung
In der 9. Klasse Mathe der Realschule lernst du die Abbildung der zentrischen Streckung. Du kennst bereits von der 6. Klasse die Achsenspiegelung und aus der 7. Klasse die Parallelverschiebung. Im Mathezweig lernt du in der 8. Klasse noch eine weitere Abbildung, die Drehung.
Bei der Achsenspiegelung, der Parallelverschiebung und der Drehung handelt es sich um Kongruenzabbildungen.
Bei einer Kongruenzabbildung sind Urfigur (ursprüngliche Figur) und die Bildfigur (neu enstandene Figur) deckungsgleich, also kongruent. Bei der zentrischen Streckung ist dies nicht der Fall, wie du auch am Beispiel des Baumes sehen kannst. Die Urfigur wird vergrößert oder auch verkleinert durch die zentrische Streckung. Bei der zentrischen Streckung handelt es sich stattdessen um eine Ähnlichkeitsabbildung.
Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen und nützliche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe hier online Mathe.
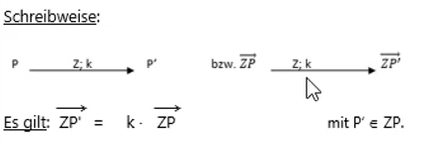
Zentrische Streckung und die Abbildungsvorschrift (Schreibweise für die Abbildung)
Für die zentrische Streckung wird ein Streckungszentrum Z benötigt. Der Punkt Z ist der Punkt, von dem aus gestreckt wird. Der Streckungsfaktor k gibt an, um welchen Faktor gestreckt wird. Um zu wissen wie lang die Bildstrecke vom Zentrum bis zum Bildpunkt z.B. A‘, B‘ usw. ist, musst du die Länge der Urstrecke vom Zentrum bis A, B usw. mit dem Streckungsfaktor k multiplizieren.
Für k = 1 gilt, dass die Ur- und die Bildstrecke gleich lang sind, da mit dem Faktor 1 multipliziert wird. Für diesen Sonderfall sind Ur- und Bildfigur kongruent.
Für k = -1 gilt, dass Ur- und Bildstrecke gleich lang sind, jedoch auf verschiedenen Seiten vom Zentrum liegen.
Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du anschauliche Mathe-Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter mit Matheaufgaben zum Ausdrucken.
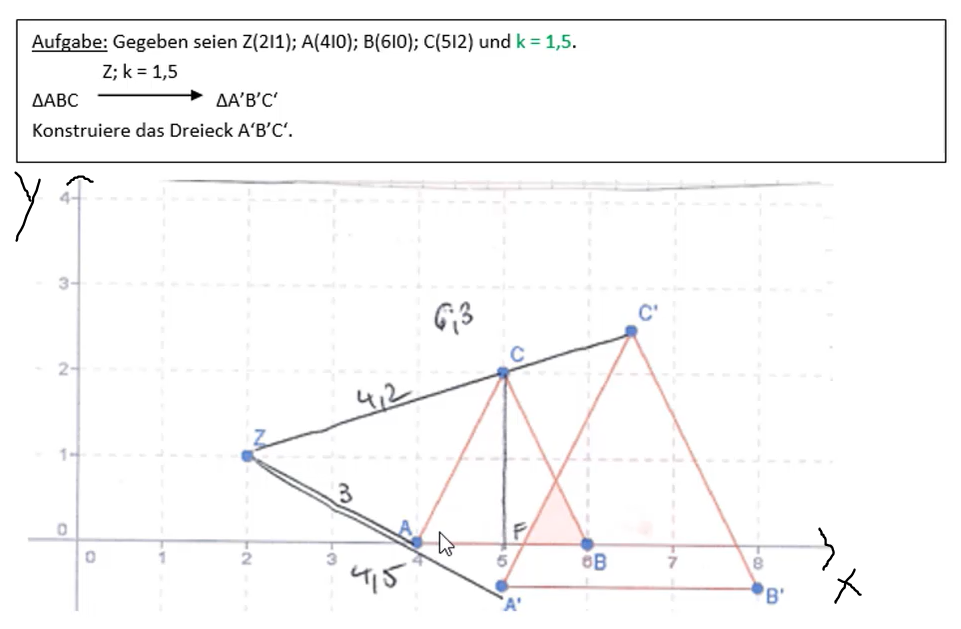
Beispiel: So gehst du vor, wenn du eine zentrische Streckung durchführst
Trage zunächst die gegebenen Punkte Z, A, B und C in ein Koordinatensystem ein. Du weißt nun, dass die Urfigur ein Dreieck ist, das durch zentrische Streckung mit dem Zentrum Z und dem Streckungsfaktor
k = 1,5 zentrisch gestreckt werden soll.
Miss nun die Länge von Z nach A. Die Länge dieser Urstrecke musst du nun mit 1,5 multiplizieren, damit du die Länge der Bildstrecke von Z nach A‘ weißt.
Miss anschließend die Länge von Z nach B. Auch diese Urstrecke musst du mit dem Faktor k multiplizieren, hier 1,5.
So gehst du auch mit dem Urpunkt C vor, wenn du C‘ abbilden möchtest.
Diese Vorgehensweise gilt für alle Urfiguren.
Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Drucken. Übe hier online Mathe mit einer Realschullehrerin.
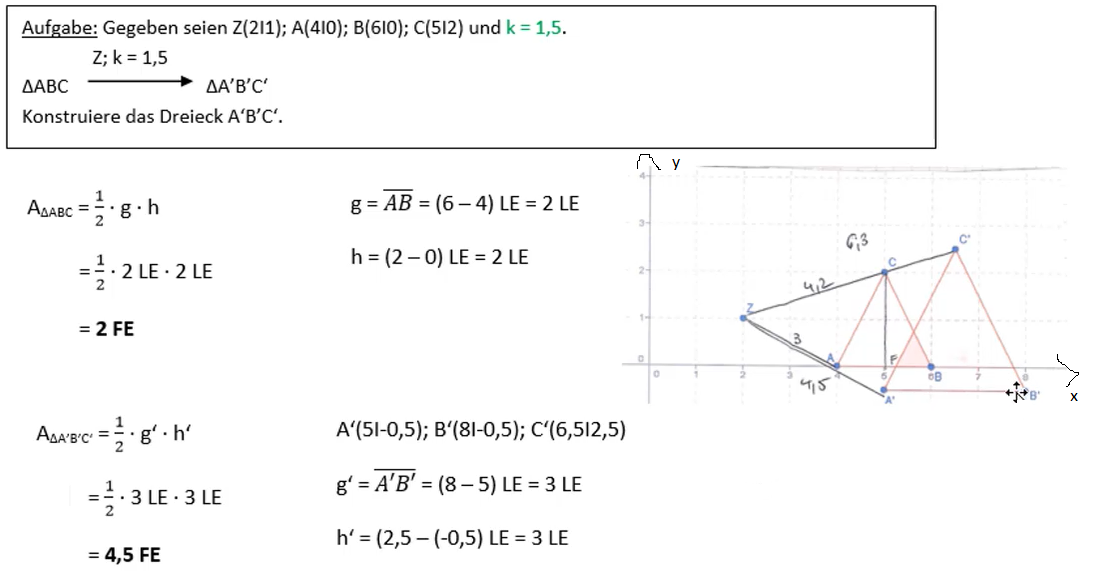
Flächeninhalt bei einer zentrischen Streckung
Wie du bereits weißt, ist die zentrische Streckung keine Kongruenzabbildung, da Ur- und Bildfigur sich durch diese Abbildung in ihrer Größe ändern. Nur für den Sonderfall k = 1 und k = -1 bleibt die Fläche von Ur- und Bildfigur unverändert.
Die Veränderung der Fläche von Ur- und Bildfigur ist nicht zufällig, sondern es liegt ein Zusammenhang vor.
In diesem Beispiel siehst du, dass der Flächeninhalt der Urfigur 2 FE (Flächeneinheiten) beträgt, du arbeitest mit der Formel A = 1/2 * g*h, da es sich bei der Urfigur um ein Dreieck handelt.
Der Flächeninhalt der Bildfigur ergibt 4,5 FE (Flächeneinheiten).
Du siehst also, dass die Fläche der Urfigur stets mit k² multipliziert wird, um die Fläche der Bildfigur zu erhalten.
In unserem Beispiel gilt k = 1,5, somit wurde mit 1,5² multipliziert.
Warum k²?
Du siehst bei der allgemeinen Herleitung der Formel, dass die Bildstrecke g‘ sich aus k* g ergibt.
Auch die Höhe h‘ der Bildfigur hat sich durch k*h ergeben.
Wird nun die Formel
A = 1/2*g’*h‘ verwendet, wurden zwei Urstrecken ver-k-facht, sodass mit dem Faktor k² gerechnet werden muss.
Die Formel ABildfigur = k² * A Urfigur gilt für alle zentrischen Streckungen und alle Urfiguren.
Entdecke diese Lernplattform und tauche ein in die faszinierende Welt des Mathematikunterrichts! Hier erwartet dich eine Vielzahl von interaktiven Erklärvideos, herausfordernden Übungen und praktischen Arbeitsblättern mit Matheaufgaben, die dir dabei helfen, Mathe online zu meistern.
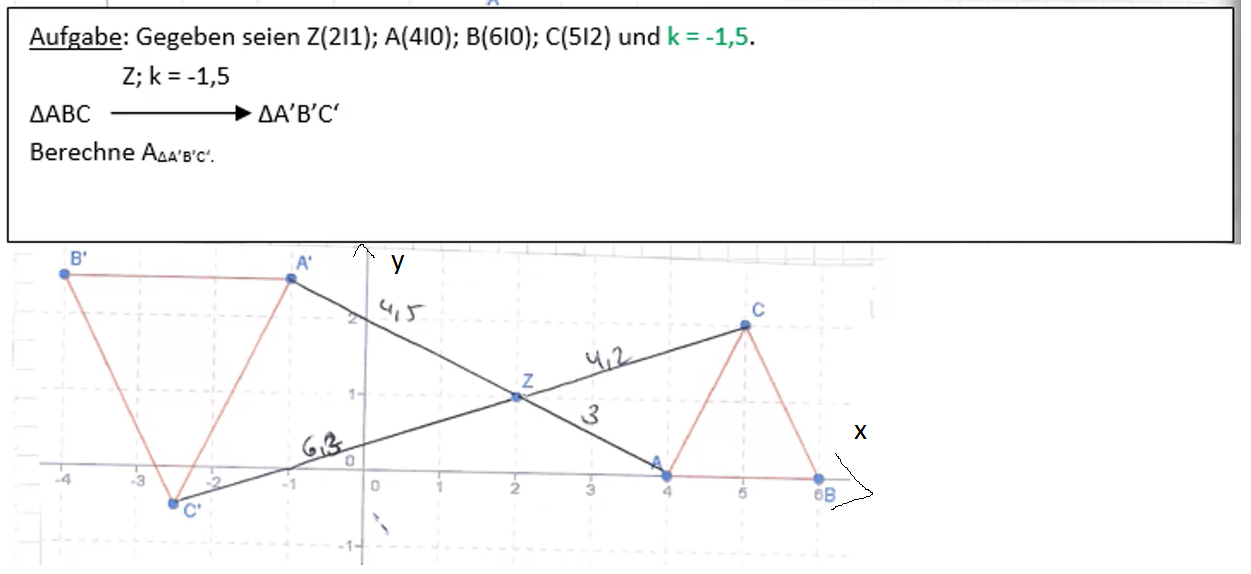
Zentrische Streckung mit negativem Streckungsfaktor k
In diesem Beispiel gilt der negative Streckungsfaktor
k = -1,5.
Miss die Länge der Urstrecke von Z nach A. Diese Länge wird nun mit dem Faktor 1,5 (Der Betrag von I-1,5I = 1,5) multipliziert. Die Länge der Bildstrecke von Z nach A‘ wird nun angetragen. Beachte dabei, dass stets Urpunkt, Bildpunkt und das Zentrum Z auf einer Gerade liegen.
Ist der Streckungsfaktor k negativ, so müssen Ur-und Bildpunkt auf verschiedenen Seiten vom Zentrum Z liegen.
Jetzt verstehst du bestimmt auch, warum für den Sonderfall k = -1 Ur -und Bildfigur gleich groß bleiben, jedoch auf verschiedenen Seiten vom Zentrum Z liegen.
Mithilfe dieser Formel kann ganz schnell der Flächeninhalt der Bildfigur berechnet werden, wenn du den Flächeninhalt der Urfigur und den Streckungsfaktor k weißt. Es kann gut sein, dass du zunächst den Flächeninhalt der Urfigur rechnerisch ermitteln musst.
Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe hier online Mathe.
Fit in die Mathe-Abschlussprüfung Mathematik (Realschule Bayern) - Prüfungsvorbereitung online (10. Klasse - 10II/III)
Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung - Starte gleich los!
