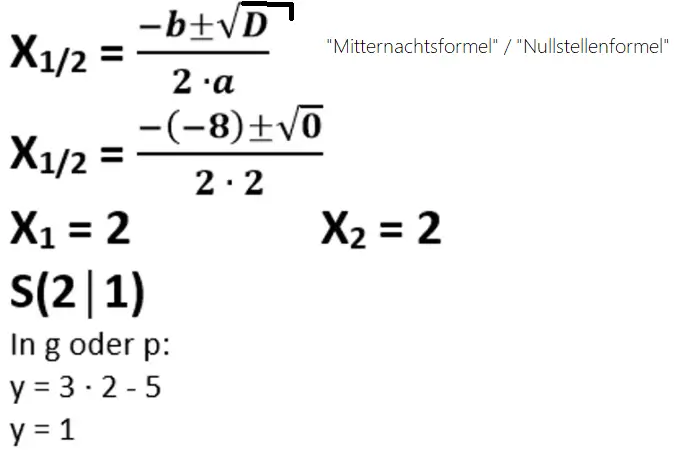Schnittpunkte berechnen: Zwei Schnittpunkte (Diskriminante positiv)

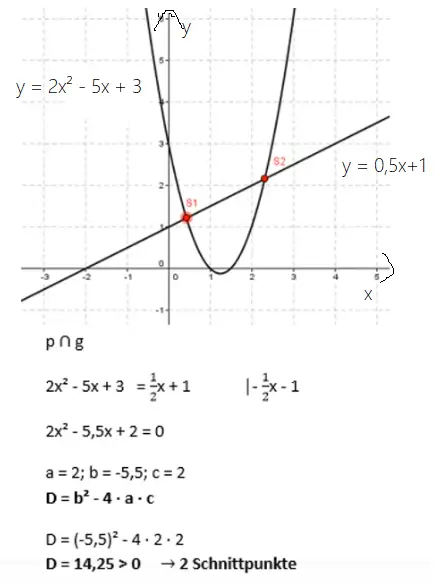
In diesem Beispiel sind die Funktionsgleichung einer Parabel p und die einer linearen Funktion g gegeben. Du siehst bereits in der Zeichnung, dass sich die beiden Graphen von p und g in zwei Schnittpunkten schneiden. Die Gerade wird als Sekante bezeichnet, da zwei Schnittpunkte vorliegen.
In der 10. Klasse Mathematik (Realschule Bayern) lernst du wie du die Schnittpunkte rechnerisch ermitteln kannst:

Um die Koordinaten von Schnittpunkten zu berechnen, verwendest du die „Mitternachtsformel“ / „Nullstellenformel“.
So gehst du vor:
– Schritt 1: Setze p und g gleich
d.h. 2x² – 5x + 3 = 0,5x + 1
– Schritt 2: Forme die Gleichung so um, dass auf einer Seite 0 steht.
– Schritt 3: Nun kannst du a, b und c ablesen.
– Schritt 4: Berechne nun die Diskriminante D mit der Formel D = b² – 4ac.
Ist D > 0, so liegen 2 Schnittpunkte vor.
Ist D = 0, so gibt es einen Schnittpunkt.
Ist D < 0, so gibt es keinen Schnittpunkt.

In diesem Beispiel ist D > 0 und somit weißt du auch rechnerisch, dass es zwei Schnittpunkte von Parabel und Gerade gibt. Bei Schnittpunkten von Parabel und Parabel ist die Vorgehensweise identisch.

Setzt du nun in die „Mitternachtsformel“ / „Nullstellenformel die Werte für a, b und die Diskriminante ein, so kannst du die x-Werte der Schnittpunkte ermitteln. Nachdem die Schnittpunkte auf der Parabel und auch auf der Gerade liegen, kannst du im Anschluss die beiden x-Werte entweder in die Parabelgleichung oder in die Geradengleichung einsetzen, um die beiden y-Werte zu erhalten. Sind die Koordinaten der Schnittpunkte verlangt, so benötigst du immer den x-Wert und auch den y-Wert. Denn es gilt: S1(x1/y1) und S2(x2/y2).

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Lerne Mathe online.

Schnittpunkt berechnen: Ein Schnittpunkt (Diskriminante =0)

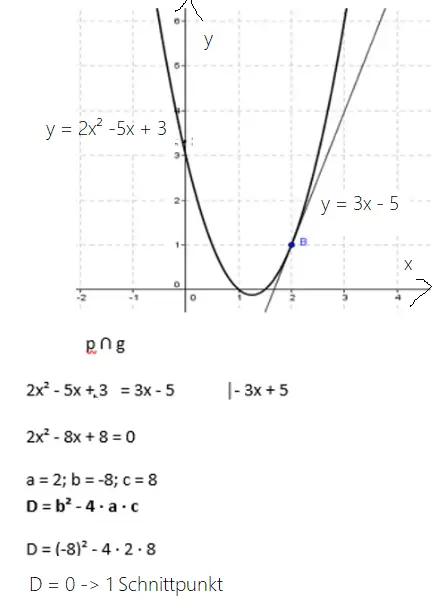
Du siehst hier in der Zeichnung, dass sich die gegebene Parabel und Gerade in einem Punkt berühren (Berührpunkt). Es liegt somit eine Tangente vor. Mithilfe der „Mitternachtsformel“ / „Nullstellenformel“ ist es möglich die Koordinaten dieses Berührpunkts rechnerisch zu ermitteln.
Setze hierzu wieder die beiden Funktionsgleichungen (von p und g) gleich und löse die Gleichung so auf, dass 0 auf einer Seite der Gleichung steht.
Wenn du nun die Diskriminante D berechnest, ergibt sich: D = 0. Dieses Ergebnis kommt immer raus, wenn es sich bei der Gerade um eine Tangente handelt und genau ein Schnittpunkt / Berührpunkt vorliegt.

Mithilfe der „Mitternachtsformel“ / „Nullstellenformel“ kannst du nun den x-Wert des Berührpunkts berechnen.
x1 und x2 sind identisch, da es hier nun einen Schnittpunkt gibt, deshalb ist es gleichgültig, ob du in der Mitternachtsformel addierst oder subtrahierst.
Um den y-Wert zu berechnen, kannst du den x-Wert in p oder g einsetzen. Gib sodann die Koordinaten des Berührpunkts an und du bist fertig.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und passende Arbeitsblätter mit Matheaufgaben zum Drucken.

Schnittpunkte berechnen: Kein Schnittpunkt (Diskriminante negativ)

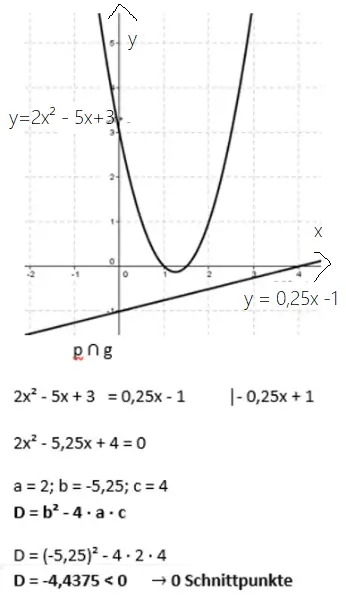
Schneiden sich die beiden Funktionsgleichungen (von p und g) nicht, so liegt eine Passante vor.
Es reicht in diesem Fall, wenn du die Diskriminante berechnest und feststellst, dass diese negativ ist.
Du braucht nun gar nicht mehr in die Mitternachtsformel einzusetzen, da Parabel und Gerade keine Schnittpunkte besitzen.
Nachdem der Radikand (der Term unter der Wurzel) in diesem Fall negativ ist, kann x1 oder auch x2 nicht berechnet werden.

Du siehst an dieser Vorgehensweise, warum es ganz praktisch ist, wenn du zunächst die Diskriminante D berechnest:
Sollte D negativ sein, bist du gleich fertig und kannst rechnerisch folgern, dass es keine Schnittpunkte gibt.

Schnittpunkte berechnen: Kein Schnittpunkt (Diskriminante negativ)

Du lernst in der 10. Klasse Mathematik der Realschule im Themenbereich „Quadratische Funktionen“, wie du alle 3 Szenarien berechnest. Das Thema ist auch prüfungsrelevant für die Abschlussprüfung im Fach Mathematik.
Du solltest deshalb alle Fälle können: 2 Schnittpunkte berechnen, ein Schnittpunkt berechnen oder zeigen, dass es keinen Schnittpunkt gibt.
Schau dir hierzu auch nochmal an, wie du Nullstellen berechnen kannst.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen und nützliche Arbeitsblätter zum Ausdrucken, um online Mathe zu üben.

Fit in die Mathe-Abschlussprüfung Mathematik (Realschule Bayern) – Prüfungsvorbereitung online (10. Klasse – 10II/III)

Ich zeige dir, welche Aufgaben immer wieder in der Abschlussprüfung (Mathe Realschule) auftauchen, sodass du dir die Punkte leicht holen kannst.
Sichere dir jetzt eine gute Note mit einer gezielten Vorbereitung – Starte gleich los!

Möchtest du auch auf Vorwissen aus den Klassen 5 bis 9 zugreifen?

Dann kombiniere den Prüfungskurs mit einem der folgenden Pakete:
1 Monat, 3 Monate oder 6 Monate.