Die Achsenspiegelung ist eine Abbildung, bei der jedem Urpunkt P (Punkt der ursprünglichen Figur) jeweils ein Bildpunkt P‘ (Punkt der Figur nach der Abbildung) zugeordnet wird. Die Zuordnung erfolgt durch die Spiegelung an einer Spiegelachse (=Gerade).
Während die Urfigur gegen den Uhrzeigersinn beschriftet wird, ist die Bildfigur durch die Achsenspiegelung im Uhrzeigersinn benannt. Das bedeutet, dass sich durch die Achsenspiegelung der „Umlaufsinn“ (also die Richtung der Beschriftung) verändert.

Willkommen auf dieser hilfreichen Lernplattform, wo Mathematik zum spannenden Abenteuer wird. Tauche ein in eine Welt voller interaktiver Übungen, mitreißender Erklärvideos und praktischer Arbeitsblätter.

Eigenschaften der Achsenspiegelung

Bei der Achsenspiegelung, die in der 6. Klasse des Lehrplans der Realschule Bayern behandelt wird, handelt es sich um eine Kongruenzabbildung. Das bedeutet, dass die Urfigur und die entstandene Bildfigur deckungsgleich (=kongruent) sind.

Die Achsenspiegelung besitzt folgende Eigenschaften:

• Ur- und Bildfigur sind längentreu, d.h. die Länge von den jeweiligen Ur- und Bildstrecken bleibt erhalten.
• Ur- und Bildfigur sind winkeltreu, d.h. die Winkelmaße bleiben erhalten.
• Ur- und Bildfigur sind geradentreu.
• Ur- und Bildfigur sind kreistreu, d.h. Ur- und Bildkreis haben den gleichen Radius.
• Ur- und Bildfigur sind parallelentreu, d.h. parallele Strecken sind auch in der Bildfigur parallel.

In der 9. Klasse lernst du in Mathe an der Realschule eine Abbildung kennen, bei der es sich um keine Kongruenabbildung handelt, sondern um eine Ähnlichkeitsabbildung. Es geht um die zentrische Streckung, alle anderen Abbildungen, die die noch lernst, sind Kongruenzabbildungen.

Was ist ein Fixpunkt?

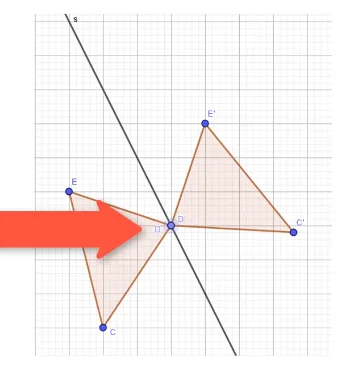
Bei einem Fixpunkt handelt es sich um einen Punkt, der auf sich selbst abgebildet wird. Ur- und Bildpunkt sind demnach identisch, hier D = D‘.

Die Spiegelachse als Fixpunktgerade

Alle Punkte, die sich auf der Spiegelachse befinden werden durch die Achsenspiegelung auf sich selbst abgebildet, sodass die Spiegelachse aus unendlich vielen Fixpunkten besteht. Die Spiegelachse wird deshalb auch als Fixpunktgerade bezeichnet.

Unterschied Fixpunktgerade und Fixgerade

Wird eine Gerade, die senkrecht zur Spiegelachse verläuft, gespiegelt, so wird diese Gerade auf sich selbst abgebildet. Ur- und Bildgerade stimmen somit überein (g = g‘), es handelt es sich um eine Fixgerade. Die einzelnen Ur- und Bildpunkte auf der Gerade sind nicht identisch. Während bei einer Fixpunktgerade alle Ur- und Bildpunkte übereinstimmen, sind bei einer Fixgerade Ur- und Bildfigur im Gesamten identisch.

Auf dieser Lernplattform entdeckst du die Welt der Mathematik online: Hier findest du inspirierende Erklärvideos, herausfordernde interaktive Übungen und nützliche Arbeitsblätter, die du bequem ausdrucken kannst.