Potenzfunktionen gehören zu den wichtigsten Funktionsarten in der Mathematik. Sie treten überall auf – von einfachen Quadratzahlen bis zu komplexen Wurzeln. Auf dieser Seite lernst du alles, was du für Schule, Prüfung und Übungen zu Potenzfunktionen brauchst: Definition, Eigenschaften, Beispiele und Tipps zur Lösung.

Was ist eine Potenzfunktion?

Eine Potenzfunktion ist eine Funktion der Form

$$f(x) = x$$

wobei

• x die Variable (Eingabewert) ist,

• n der Exponent ist (z. B. 2, 3, –1, ½),

• f(x) das Ergebnis ist.

👉 Kurz gesagt: Eine Potenzfunktion hebt eine Zahl $x$ zu einer bestimmten Potenz $n$. Bei einer Potenzfunktion taucht die Variable z.B. x immer in der Basis auf.

Man unterscheidet bei Potenzfunktionen zwischen denen mit einem geraden bzw. einem ungeraden Exponent. Die Grafik zeigt das typische Aussehen der Potenzfunktionen. Während Potenzfunktionen mit geraden Exponenten z.B. 2; 4; 6 usw. achsensymmetrisch zur y-Achse verlaufen, sind Potenzfunktionen mit ungeraden Exponenten z.B. 3; 5; 7 usw. punktsymmetrisch. Für die Variable x dürfen alle Werte aus dem Definitionsbereich (Menge IR) eingesetzt werden.

Gerade und ungerade Exponenten

Potenzfunktionen mit geradem Exponenten

$f(x)=x^{\mathrm{n }}$$\mathrm{mit\; n}=\mathrm{2;}\mathrm{4;6;}\dots$

Für solche Funktionen gilt: Positive und negative x-Werte liefern denselben Funktionswert, da beim Potenzieren mit einem geraden Exponenten das Vorzeichen verschwindet. Der Graph ist deshalb achsensymmetrisch zur y-Achse. Außerdem gilt für alle geraden Exponenten:
Der Funktionswert ist nie negativ. Die Parabel (z. B. bei

$f(x)=x^2$öffnet sich nach oben und besitzt ihr Minimum im Ursprung oder oberhalb davon.

👉 Merke:
Potenzfunktionen mit geradem Exponenten sind achsensymmetrisch zur y-Achse.

Potenzfunktionen mit ungeradem Exponenten

$f(x)=x^{\mathrm{n }}$$\mathrm{mit\; n}=1;3;\; 5;\; 7;\dots$

Hier bleibt das Vorzeichen von x erhalten: Positive x-Werte führen zu positiven Funktionswerten, negative x-Werte zu negativen Funktionswerten.

Der Graph ist deshalb punktsymmetrisch zum Ursprung.
Typisch ist ein S-förmiger Verlauf, z. B. bei $f(x)=x^3$bei dem der Graph den Ursprung durchläuft und stetig steigt.

 👉 Merke:
Potenzfunktionen mit ungeradem Exponenten sind punktsymmetrisch zum Ursprung.

Dieser Inhalt ist Teil des Prüfungskursesund bereitet dich gezielt auf die Mathematik-Abschlussprüfung der Realschule Bayern vor.

Arten von Potenzfunktionen

Es gibt verschiedene Arten von Potenzfunktionen – abhängig davon, ob der Exponent natürlich, ganzzahlig oder rational ist.

Potenzfunktionen mit natürlichen Exponenten

Beispiele:

• $f(x) = x^2$

  (Quadratische Funktion → Parabel)

• $f(x) = x^3$

  (Kubikfunktion)

• $f(x)=x^4,x^5,$

  …

Eigenschaften:

• Gerade Exponenten → Achsensymmetrisch zur y-Achse

• Ungerade Exponenten → Punktsymmetrisch zum Ursprung

Hier erwarten dich verständliche Mathe-Lernvideos, interaktive Übungen und praktische Arbeitsblätter mit Matheaufgaben zum direkten Ausdrucken. Lerne und übe hier online Mathe mit einer Realschullehrerin.

Potenzfunktionen mit ganzzahligen Exponenten

 Allgemein:

$$f(x) = x^{-n} = \frac{1}{x^n$$

​

• Ganzzahliger Exponent bedeutet, dass im Exponent eine Zahl aus der Menge Z stehen darf. Z =  {…;-2; -1; 0; 1; 2; 3…}

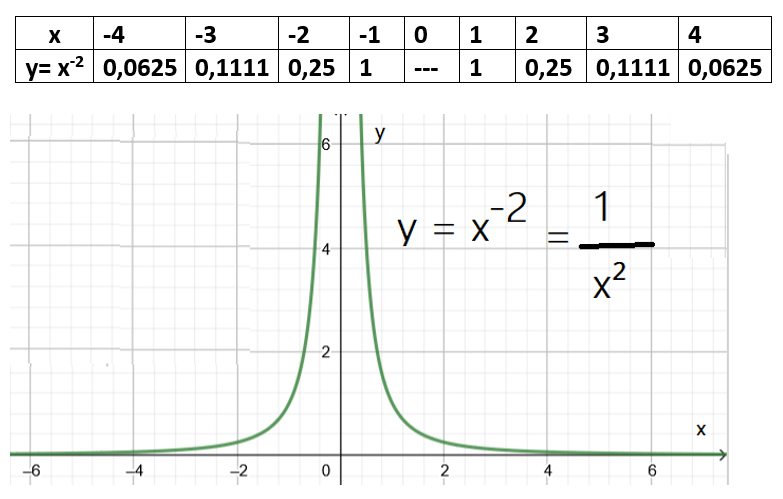
• Nachdem die Variable x im Nenner steht, muss beachtet werden, dass der Nenner nicht 0 annehmen darf. Somit gilt: Für

  $x=0$

   nicht definiert (Division durch 0 verboten).

• y-Achse ist Asymptote. Der Graph der Funktion nähert sich beliebig nahe an die y-Achse (x = 0) an, auf der Achse liegt jedoch kein Punkt des Graphen.

Beispiel:

$f(x) = \frac{1}{x^2}$

oder

$f(x) = \frac{1}{x^3}$

Potenzfunktionen mit rationalen Exponenten

Außerdem werden im Mathezweig (10. Klasse; Mathe Realschule Bayern) Potenzfunktionen mit rationalen Exponenten behandelt. Hierbei können im Exponent Werte aus der Zahlenmenge Q (Rationale Zahlen) stehen. Du siehst auf dem Bild z.B 1/2 oder 1/3. Anstelle dieser Schreibweise kann eine entsprechende Wurzelschreibweise verwendet werden.

Dieser Inhalt ist Teil des Prüfungskursesund bereitet dich gezielt auf die Mathematik-Abschlussprüfung der Realschule Bayern vor.

Potenzfunktionen zeichnen

1. Bestimme die Definitionsmenge.

2. Setze einige x-Werte ein und berechne $\mathrm{f(x).}$

3. Beachte Symmetrie-Eigenschaften (gerade/ungerade Exponenten).

4. Zeichne den Graphen im Koordinatensystem.

👉 Tipp: Nutze Tabellen und markiere wichtige Punkte wie (1|1), (–1|1) oder Asymptoten.

Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und passende Arbeitsblätter mit Matheaufgaben zum Drucken und Üben.