Lagebeziehung von Kreis und Gerade: Passante, Sekante, Tangente – Lernvideos und Aufgaben (Mathe 7. Klasse)

Die drei Lagebeziehungen von Kreis und Gerade

In der Realschule lernst du in der 7. Klasse Mathematik im Themenbereich
„Geometrische Ortslinien und Ortsbereiche“ die Lagebeziehung von Kreis und Gerade kennen.
Dabei gibt es genau drei Möglichkeiten, wie ein Kreis und eine Gerade zueinander liegen können.

Möglichkeit 1: Passante
→ Kreis und Gerade schneiden sich nicht (kein Schnittpunkt)

Möglichkeit 2: Sekante
→ Kreis und Gerade schneiden sich in zwei Punkten (2 Schnittpunkte)

Möglichkeit 3: Tangente
→ Kreis und Gerade berühren sich in genau einem Punkt (1 Berührpunkt)

Entdecke die Welt der Mathematik online: Dich erwarten verständliche Lernvideos, interaktive Übungen und praktische Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Passante: Kreis und Gerade schneiden sich nicht (Möglichkeit 1)

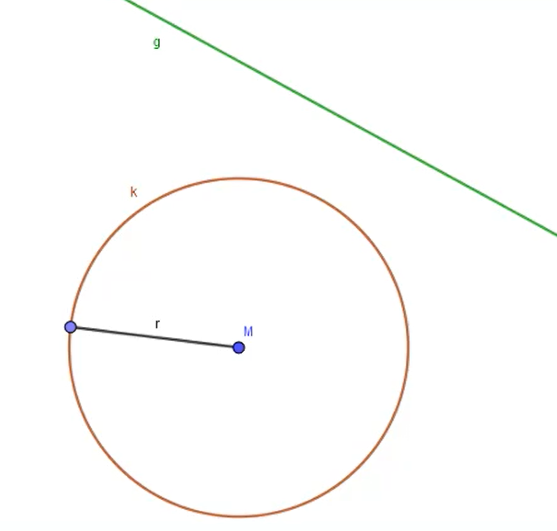
Kreis und Gerade können so zueinander liegen, dass sich diese in keinem Punkt schneiden. Wie das dann beispielsweise aussieht, siehst du auf dem Bild. Schneiden sich Kreis und Gerade nicht, so wird die Gerade als Passante bezeichnet.

Auf dieser Lernplattform wirst du Mathe online spielend leicht meistern: Hier findest du anschauliche Mathe-Lernvideos, interaktive Übungen und sorgfältig erstellte Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

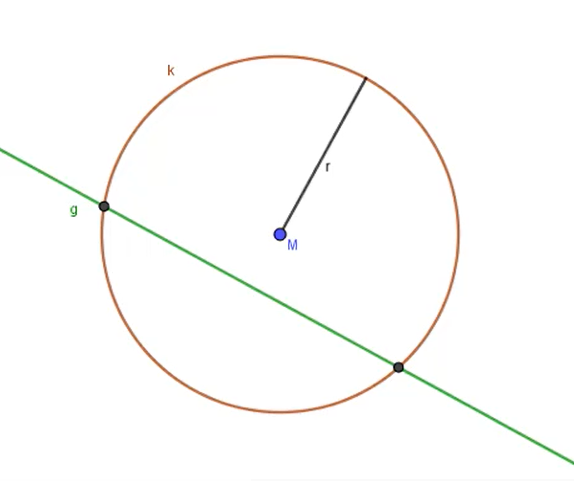
Sekante: Kreis und Gerade schneiden sich in zwei Punkten (Möglichkeit 2)

Verläuft die Gerade so, dass diese den Kreis zweimal schneidet, handelt es sich bei der Gerade um eine Sekante.
Du siehst auf dem Bild, wie in diesem Fall dann die Gerade und der Kreis zueinander liegen.

Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen und nützliche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

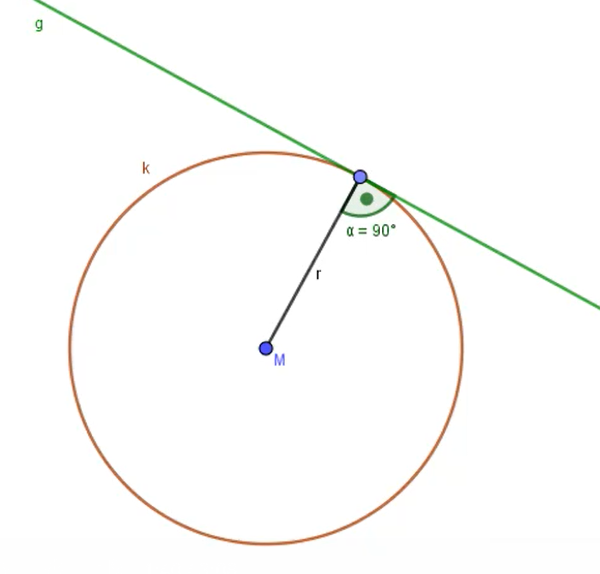
Tangente: Kreis und Gerade berühren sich in einem Punkt (Möglichkeit 3)

Eine Tangente liegt genau dann vor, wenn die Gerade so verläuft, dass diese den Kreis in genau einem Punkt berührt (1 Berührpunkt). Bei jeder Tangente bildet der Radius des Kreises mit der Gerade einen rechten Winkel (90°). Diese Tatsache verwendest du, wenn du mithilfe eines Geodreiecks die Tangente zeichnen möchtest.

So konstruierst du die Tangente (mit Zirkel und Geodreieck)

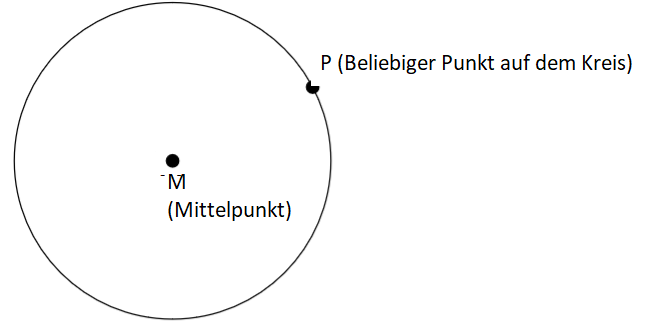
Schritt 1:
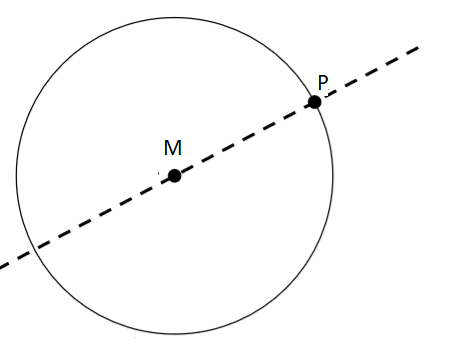
Möchtest du mithilfe eines Zirkels eine Tangente konstruieren, so markierst du einen beliebigen Punkt auf der Kreislinie. (Hier: Punkt P)

Schritt 2:
Zeichne eine Gerade ein, die durch den Kreismittelpunkt M und den gesetzten Punkt P verläuft.

Schritt 3:
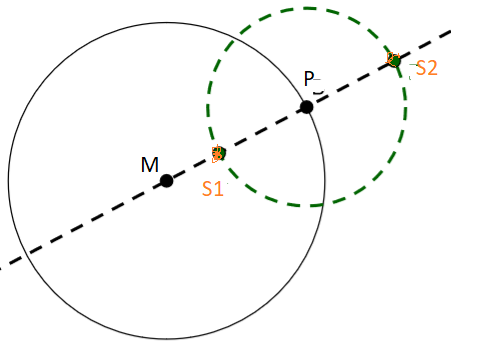
Stich mit dem Zirkel in den Punkt P ein. Der Punkt P ist der Kreismittelpunkt eines Kreises, den du nun einzeichnest. Den Radius kannst du beliebig wählen. Markiere die beiden Schnittpunkte (hier: S1 und S2) der Kreislinie mit der Gerade.

Entdecke eine innovative Lernplattform für Mathe: Hier findest du interaktive Mathe-Lernvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken.

Schritt 4:
Konstruiere nun eine Mittelsenkrechte. Wie das geht hast du in Mathe an der Realschule in der 6. Klasse gelernt. Eine detaillierte Erklärung findest du auch hier.
Stich mit dem Zirkel in den Schnittpunkt S1 ein, zeichne einen Halbkreis. Der Radius des Halbkreises muss groß genug sein. (muss über den Mittelpunkt der Strecke von S1 nach S2 hinausgehen)
Stich nun mit dem Zirkel in den anderen Schnittpunkt, S2, ein und ziehe mit dem gleichen Radius einen weiteren Halbkreis.
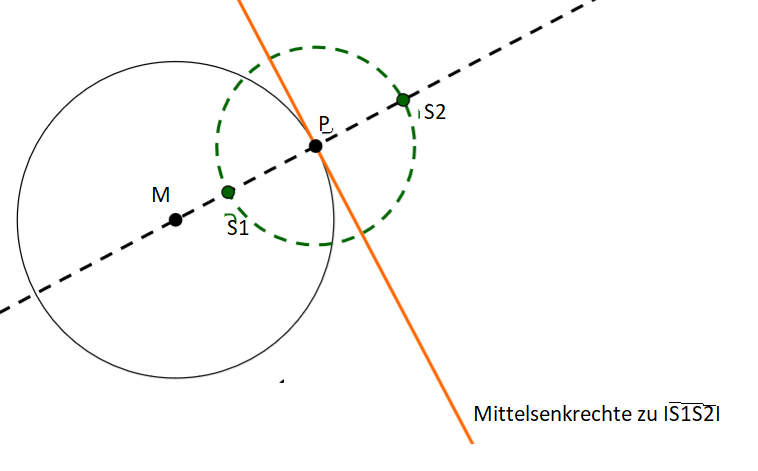
Durch die beiden Schnittpunkte der Halbkreise verläuft nun die Mittelsenkrechte. Diese Mittelsenkrechte ist die gesuchte Tangente an den Kreis.
Zur Kontrolle: Die Tangente muss im rechten Winkel zum Radius des ursprünglichen Kreises (mit Mittelpunkt M) sein.

So kannst du rechnerisch bestimmen, ob eine Sekante, Passante oder Tangente vorliegt

In der 7. Klasse Realschule werden die Lagebeziehungen von Kreis und Gerade zeichnerisch untersucht. Die rechnerische Bestimmung mithilfe der Diskriminante ist Bestandteil der 10. Klasse.
Dies kann auch für Gerade und Gerade, Parabel und Parabel bzw. Gerade und Parabel angewendet werden. Doch dazu in der 10. Klasse mehr.
Mithilfe der Diskriminante kannst du erkennen, ob es sich um eine Sekante, Passante oder Tangente handelt.
Ist die Diskriminante D positiv, also gilt D>0, so liegt eine Sekante vor.
Ist die Diskriminante D negativ, also gilt D<0, so liegt eine Passante vor.
Ist die Diskriminante D gleich 0, also gilt D=0, so liegt eine Tangente vor.

Lerne Mathematik online mit anschaulichen Erklärvideos, interaktiven Übungen und hilfreichen Arbeitsblättern, die du ganz einfach ausdrucken kannst.