Innenwinkelsumme im Dreieck – Lernvideos und Aufgaben (Mathe 7. Klasse)
Was bedeutet „Innenwinkelsumme“?
Grübelst du gerade, was wohl der Begriff „Innenwinkelsumme“ bedeutet? Ich kann dich gleich erlösen, du wirst sehen, das Thema kann sehr leicht sein.
Jedes Dreieck hat drei Eckpunkte. An jedem Eckpunkt befindet sich ein Winkel.
Diese Winkel liegen innerhalb des Dreiecks und heißen deshalb Innenwinkel.
Addiert man alle drei Innenwinkel, ergibt sich immer 180°.
Diese feste Summe nennt man die Innenwinkelsumme.
Auf dieser Seite findest du anschauliche Erklärungen, Beispiele und Übungen zur Innenwinkelsumme im Dreieck – passend für die 7. Klasse.
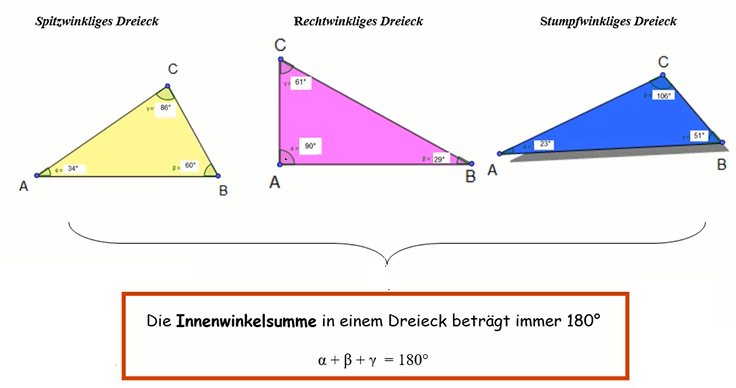
Innenwinkelsumme in spitzwinkligen, rechtwinkligen und stumpfwinkligen Dreiecken
Spitzwinkliges Dreieck – Innenwinkelsumme
Ein Dreieck ist spitzwinklig, wenn alle drei Winkel kleiner sind als 90°. In diesem Beispiel haben die Winkel, 34°, 60° und 86°. Die Summe der drei Winkel muss immer 180° ergeben. So kannst du auch jederzeit, wenn nur zwei Winkel bekannt sind, den fehlenden dritten Winkel berechnen.
Rechtwinkliges Dreieck – Innenwinkelsumme
Ein Dreieck ist rechtwinklig, wenn ein rechter Winkel (=90°) vorliegt. Jetzt verstehstu du auch warum ein Dreieck nur genau einen rechten Winkel haben kann. Wären zwei rechte Winkel vorhanden, so hätten diese zusammen bereits 180°. Nachdem ein Dreieck aber immer aus drei Winkeln besteht, würde dieses Dreieck nicht existieren. In unserem Beispiel haben die einzelnen Winkel 90°, 29° und 61°. Auch in einem rechtwinkligen Dreieck besitzt die Innenwinkelsumme immer 180°.
Stumpfwinkliges Dreieck – Innenwinkelsumme
Ein Dreieck ist stumpfwinklig, wenn ein Winkel größer als 90° ist. In unserem Beispiel hat der stumpfe Winkel 106°. Aufgrund der Innenwinkelsumme kann nur ein stumpfer Winkel dabei sin, da sonst die Innenwinkelsumme von 180° überschritten werden würde.
106°, 23° und 51° ergeben exakt 180°, so muss es immer sein, auch in allen stumpfwinkligen Dreiecken.
Entdecke eine innovative Lernplattform für Mathe:
Interaktive Erklärvideos, abwechslungsreiche Übungen und hilfreiche Arbeitsblätter mit Matheaufgaben zum Ausdrucken. Übe jetzt online Mathe.
Beweis für die Innenwinkelsumme im Dreieck
Idee des Beweises (Parallele durch einen Eckpunkt)
Um die Innenwinkelsumme im Dreieck zu beweisen, zeichnen wir durch einen Eckpunkt des Dreiecks eine Gerade, die parallel zur gegenüberliegenden Seite verläuft. Dadurch entstehen an dieser Parallelen neue Winkel, die wir mit den Innenwinkeln des Dreiecks vergleichen können. Diese Konstruktion hilft uns, bekannte Winkelbeziehungen zu nutzen.
Wechselwinkel erklären
Verläuft eine Gerade parallel zu einer anderen und wird sie von einer schrägen Linie geschnitten, entstehen sogenannte Wechselwinkel. Diese Winkel sind immer gleich groß. Da die neu gezeichnete Parallele zur Dreiecksseite parallel ist, sind die entstehenden Winkel an der Parallelen genauso groß wie die entsprechenden Innenwinkel des Dreiecks.
Warum ergibt sich genau 180°?
Alle Winkel entlang einer geraden Linie ergeben zusammen immer 180° (gestreckter Winkel). An der eingezeichneten Parallelen liegen die drei Winkel nebeneinander auf einer Geraden. Da diese Winkel den drei Innenwinkeln des Dreiecks entsprechen, folgt daraus:
Die Summe der Innenwinkel im Dreieck beträgt immer 180°.
Diese Lerninhalte sind speziell auf Mathematik in der 7. Klasse der Realschule abgestimmt. Du lernst Schritt für Schritt genau das, was im Unterricht verlangt wird – ideal zum Wiederholen, Üben und zur Vorbereitung auf Schulaufgaben.