Exponentialgleichungen lösen mit Logarithmen – Lernvideos und Aufgaben (Mathe 10. Klasse)
Was ist eine Exponentialgleichung?
Eine Gleichung enthält immer ein „=“. Wie du diese mithilfe von Äquivalenzumformungen lösen kannst, lernst du in der Realschule bereits in der 6. Klasse. In der 10. Klasse Mathematik (Realschule Bayern) lernst du wie du Exponentialgleichungen lösen kannst.
Eine Gleichung wird als Exponentialgleichung bezeichnet, wenn die Variable (Unbekannte) z.B. x im Exponent auftaucht.
Dieses Beispiel zeigt eine Exponentialgleichung:
Beispiel für eine Exponentialgleichung
Dieser Inhalt ist Teil des Prüfungskursesund bereitet dich gezielt auf die Mathematik-Abschlussprüfung der Realschule Bayern vor.
Exponentialgleichung mit dem Logarithmus lösen – So geht’s
Ziel einer Gleichung ist es immer, dass die Variable z.B. x auf einer Seite vom „=“ alleine steht.
Beim Lösen jeder Exponentialgleichung gilt nun: Steht die Variable im Exponent, so benötigst du für die Äquivalenzumformung den Logarithmus.
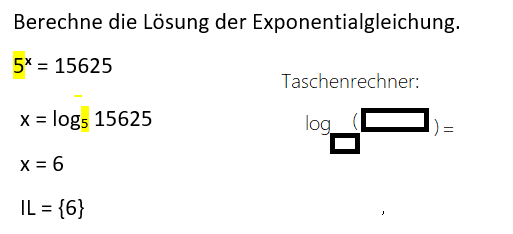
Der Logarithmus bewirkt, dass die Variable alleine steht und auf der rechten Seite der Gleichung nun der Logarithmus von 15625 zur Basis 5 berechnet wird. Wenn du in den Taschenrechner die Basis und den Wert der rechten Seite eintippst, weißt du den Wert für die Variable.
In diesem Beispiel ergibt sich für x = 6. Nun musst du im letzten Schritt noch die Lösungsmenge IL angeben.
Die Probe kannst du jederzeit durchführen, indem du 5^6 = 15625 überprüfst.
Entdecke diese interaktive Lernplattform und werde zum Mathe-Profi: Hier findest du verständliche Erklärvideos, passende Übungen und nützliche Arbeitsblätter zum Ausdrucken, um online Mathe zu üben.
Logarithmen mit Taschenrechner berechnen
Allgemeine Form einer Exponentialgleichung
Bedeutung des Logarithmus
Eine Exponentialgleichung besitzt allgemein die Form
Die Basis a wird x-mal mit sich selbst multipliziert und ergibt den Wert b.
Exponentialgleichungen können mithilfe des Logarithmus gelöst werden, da dieser die Variable aus dem Exponenten „holt“. Dadurch steht die Variable allein und der Logarithmus von b zur Basis a kann mit dem Taschenrechner berechnet werden.
In der Mathematik-Abschlussprüfung (Mathe Realschule, 10. Klasse) können Exponentialgleichungen auch abgefragt werden.
Dieser Inhalt ist Teil des Prüfungskursesund bereitet dich gezielt auf die Mathematik-Abschlussprüfung der Realschule Bayern vor.
Lösung von Exponentialgleichungen mit Logarithmen
Dieses Beispiel zeigt eine weitere Exponentialgleichung. Jede Exponentialgleichung kann mit dem Logarithmus gelöst werden: x steht alleine und der Logarithmus von 4096 zur Basis 8 kann mit dem Taschenrechner rechnerisch ermittelt werden.
Für die Variable x ergibt sich sodann x = 4. Nun muss noch im letzten Schritt die Lösungsmenge IL angegeben werden.
Nachdem 4 in der Grundmenge enthalten ist, gilt IL = {4}. Wäre 4 nicht enthalten, wäre eine „leere Menge“ die richtige Antwort für die Lösungsmenge IL.
Willkommen auf dieser Lernplattform für Mathe: Hier erwarten dich interaktive Mathe-Lernvideos, spannende Übungen und passende Arbeitsblätter mit Matheaufgaben zum Drucken.